 |
 |
 |
 |
INTRODUCTION
Our perception of the universe is shaped by our optical sensors - our eyes - and also by how our brain interprets the signals that it receives from the eyes. When we view the sky with our own eyes, they are the filter through which we view the universe and which limit our perception. Our understanding of what we see is also shaped very much by our previous knowledge of the universe.
ANATOMY OF THE EYE
The eye consists of a number of structures as shown in the diagram below:
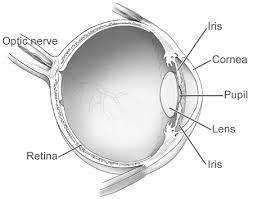
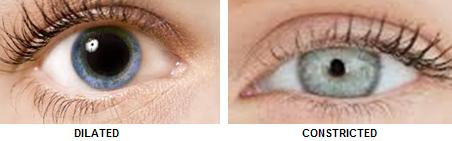
The structures at the front of the eye are responsible for focusing the light that enters the pupil onto the retina at the rear of the eyeball. Both the cornea and the lens participate in this function. The iris is able to change so that the size of the pupil varies with the intensity of light we see. In dark locations the pupil is fully dilated with a diameter of around 8 mm. In bright light the pupil is constricted down to around only 1 mm diameter.
COLOR VISION
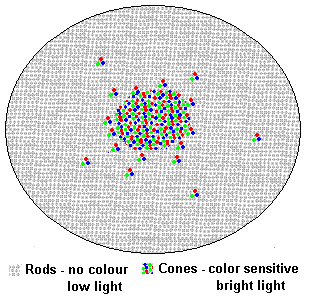
There are two sorts of visual sensors in the retina. These are called cones and rods. The cones are the sensors that are used in bright light, whereas the rods come into play in low light. Only the cones are colour sensitive, which is why the stars tend to show little colour to our eye, whereas a camera will show major colour differences between stars.
The cones are concentrated close to the central field of vision, whereas the rods are spread over the rest of the retina out to the periphery. The density of cones is also much greater in the central region than the density of rods at the periphery.
SENSITIVITY
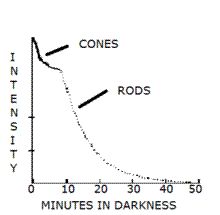
Although the eye can see over a wide range of brightness, it cannot do so instantly. We have all had the experience of being ‘blinded’ by a flash of intense light. When we go out to look at the night sky it takes a while before our eyes become ‘dark adapted’ and we are able to perceive the faintest of objects. Some of this adaptation is due to a change in the size of our pupils. From bright sunlight to dark conditions, the pupil increases in diameter from about 1 mm to almost 8 mm. This variation increases the sensitivity of the eye by 64 times. Other changes in the retina account for the rest of the adaption. This all takes time. The adaptation curve below shows that the first adaptation (to an intermediate level of sensitivity) occurs in about 10 minutes, but that the second and deeper stage of adaptation requires around half an hour. The first stage of adaptation involves the cone sensors, whereas the second stage involves the rods. Full dark adaptation takes in excess of 30 minutes, as it involves chemical processes.
To avoid the loss of dark adaptation, astronomers use soft red light to read sky charts. It should also be noted that alcohol adversely affects dark adaptation. So you might want to forego that glass of wine if you are trying to observe very faint stars, nebulae or galaxies.
Averted vision is a trick that can be used to see really faint objects. Don’t look straight at the object you wish to see. Instead, look directly off to the side, and the object you wish to see will appear brighter. The reason is that there are few rods in your central vision (this region is mainly populated by cones).
RESOLUTION
Another limit to our vision is termed resolution. This is the smallest angular distance over which we see two objects as being separate. Resolution is mainly determined by the diameter of our pupil (or telescope aperture), but also secondarily by the density of light sensors (cones and rods) across the retina.

The formula for determing resolution is:
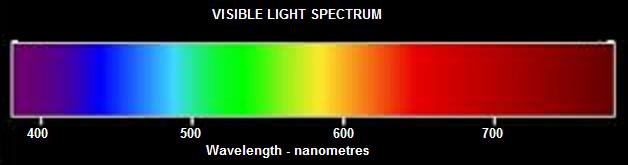
To use this formula, both the wavelength and the aperture must be in metres. Thus we must convert 8mm to 0.008 m, and 550 nm to 550 x 10-9 m.
Light varies in wavelength from 750 nm at the red end of the spectrum to about 350 nm in the violet. Our eye is most sensitive in the middle of this range and so we use a value of 550 nm in the above formula as a good compromise.
The lower the value of θ the better our resolution. For large telescopes, the resolution is limited by the atmosphere (what is termed seeing), and not the size of the telescope aperture. Only in space can the full resolution of a large telescope be realised.
Because the size of the pupil changes with light intensity, our limiting resolution also changes with the light conditions. In bright sunlight our resolution is 110 arcseconds or roughly two arcminutes. Under dark skies our theoretical resolution goes to 15 arcseconds. Due to various circumstances, including a lower density of rods at the retinal periphery, this value is unlikely to be achieved in practice for most people. However, it is interesting to note that we do have considerably better resolution at night.
STEREOPSIS
We get a perception of depth from a number of things. Having two eyes gives us an intrinsic stereopsis (stereo vision), but it can be shown that because of the limited separation of our two eyes this stereopsis is only good to a distance of less than 50 m. Many other monocular (non-stereo) cues give us (and even people with only one eye) a sense of distance. If one object lies behind another, then it must be more distant than the second object. Similar objects that appear of different sizes are generally at different distances from the beholder. As you look into the distance parallel lines converge, and the degree of convergence gives an impression of distance.
However, BEWARE! Monocular cues can be totally misleading for unfamiliar objects. It is amazing how many people (some of whom should well know better) will report an unfamiliar scenario by saying that the object plunged to ground about one kilometre away. Or that a UFO was about 10 metres in size and whizzed by less than 500 m from them.
There is absolutely no way you (or anyone else) can estimate the size and distance of an unfamiliar object in an unfamiliar situation!!! The object may be bigger than you think and further away or it may be smaller than you think and closer to you. Decption is rampart in these situations.
An experienced observer will always report the ANGULAR size of an object as that is the only possible measurement you can estimate. Angular size is measured in degrees or maybe minutes of arc (if you can compare the size to a separation between two known stars).
Most people are not experienced in estimating angular size in degrees, but can probably give a rough estimate in terms of moon angular diameters. The moon is half a degree in diameter, so if something is estimated as being ten moons wide, it is five degrees wide. If an investigator asks a lay person to estimate how long a meteor trail was in degrees, they might receive an answer of 100 degrees. But if you ask how many moons long it was, an answer of 20 moons (10 degrees) is likely to be much closer to the actual length.

Your hand held at arm's length can also be used to give rough angular estimates of an object's size. At arm's length, a single finger subtends about 2o, the hand with fingers together about 10o, and with the fingers apart about 22o.
PERCEPTION
The human eye-brain system is good at making comparisons, but it is usually woeful at estimating absolute sizes and/or distances. Even in making comparison it has to rely on the surrounding environment and past experience if the objects being compared are not close or next to one another.
One astronomical example that illustrates this is the Moon horizon illusion. When a full moon just rises above the horizon it appears to be much bigger than when the moon is viewed overhead, as in the images below.

However, the angle that the moon subtends to the observer is exactly the same in each case. A theodlite, or even a camera will show that there is no difference in the measured size of the moon (in angular diameter) in the two cases. Thus this phenomenon is not even an optical illusion (optical illusions can trick cameras equally as well as humans). This phenomenon is a psychological illusion as the effect resides entirely in the perception of the observer. When the moon is on the horizon the observer has something with which to compare, whereas when it is near the zenith there are no environmental references.
HIGH INTENSITY VIEWING
Although the eye is extremely adaptive it cannot cope with very high light intensities (such as directly viewing the Sun) and appropriate protection (through the use of filters or a projection system) must be provided. Not only should the direct light from the Sun be reduced to safe levels, but the whole face should be shaded from scattered light, and a dark environment provided to allow the pupil to dilate as much as possible to increase your resolution and allow viewing of the smallest possible sunspots.

READING
Gregory RL, Eye and Brain - the psychology of seeing, World University Library (London, 1972).
 Australian Space Academy
Australian Space Academy