A COMPUTER SEARCH FOR STELLAR ENCOUNTERS WITH THE OORT PROTO-COMET CLOUD

by Roberta Vaile

[ The material presented here represents the majority of the material contained in a thesis written for a B.Sc. (Hons) degree in 1980 at the University of Newcastle (Australia) under the supervision of Professor Colin Keay. ]

ABSTRACT

Theories on the source of the presently observed comets are discussed. A computer search was undertaken to find stars likely to perturb the Oort cloud. Two methods were used: a direct method based on parallax, proper motion and radial velocity, and Makover's 1964 method.

The results indicate that close stellar encounters have occurred in the past and will continue to occur in the future. Comparison of the methods indicate that apparently 26% of one data set of 293 stars yield the same results with either method. The principle data source used was the Royal Observatory Annals (1970). The results are intended to be first order estimates only. No concrete evidence to support the hypothesis that presently observed comets come from the Oort cloud as a result of a single close stellar encounter is apparent.

1 - INTRODUCTION

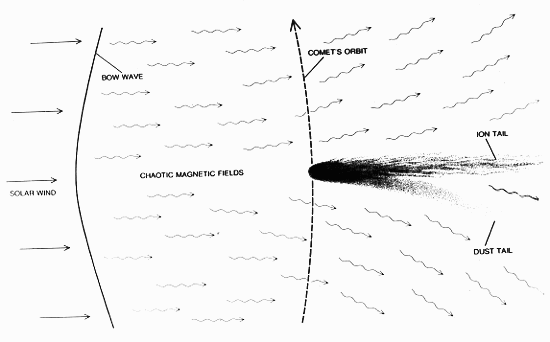
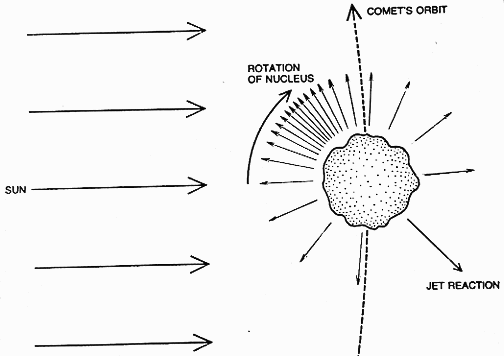
In 1866 Schiapelli identified the orbit of the Perseid meteor stream of August with that of Tuttle's comet of 1862. It was realised that in order to lose solid particles, comets must contain them instrinsically. Fine dust is also left behind comets; it scatters sunlight and is the cause of the zodiacal light seen near the plane of Earth's orbit (see Figures 1 and 2).

Figure 1: Photograph of Comet Kohoutek, 1974,
showing gas (upper) and dust (lower) tails.

A comet is comprised of a head or coma and a tail. The coma shines with sunlight scattered by dust, with reradiated sunlight from fluorescent gases or with both. Dust and gases also produce two types of tail; dust is forced out of the coma by radiation pressure from sunlight. The dust tail so formed lags behind as it streams out and so is curved. The solar wind interacts in a two-step process with the gases to produce an ion tail: high-energy electrons in the solar wind ionise the molecules in the coma, a bow-wave is produced around the coma by the solar wind and the chaotic magnetic fields accompanying the solar wind "rake out" all ionised molecules.

Figure 2: Diagram showing the production of two
different types of tail on a comet (from Whipple, 1974).

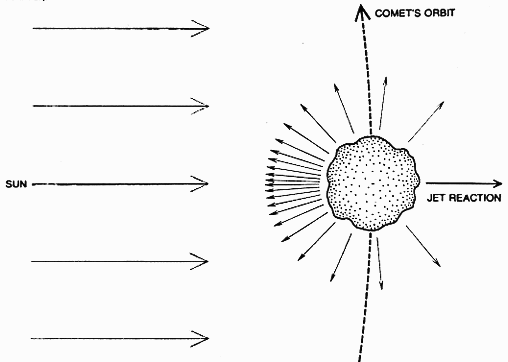
There have been two models of cometary nuclei proposed to account for the ejection of matter from comets:

(i) the 'gravel bank' model
(ii) the 'dirty snowball' model.

The 'dirty snowball' model supposes that the nucleus is a compact mass of ices interspersed with earthy material. The ices are thought to be predominantly those of water, with perhaps ammonia and methane. As the comet enters the inner solar system, the ices sublime under the action of solar radiation to produce gases in the coma and tail. The 'dirty snowball' model was proposed by Whipple in 1950.

There are three critical observational tests which the 'gravel bank' model fails while the 'dirty snowball' model satisfies. They are:

(i) the existence of a group of 'sun-grazing' comets;
(ii) the persistence of some of the periodic comets;
(iii) the detection of deviations from Newton's gravitational motion, implying the existence of nongravitational forces.

Figure 3: Comet ices sublime, sending out molecules
mostly on sunward side at speeds near 100 ms^-1.
A jet reation is thereby generated (from Whipple, 1974).

Figure 4: Comet nucleus rotating in same direction as its motion around the Sun;
jet reaction pushes comet forward in its orbit.
Comet drifts outward, orbital period increases(from Whipple, 1974).

Figure 5: Comet nucleus rotates in direction opposite to comet's direction of travel.
Comet experiences a drag force , drifts inward toward the Sun,
orbital period decreases(from Whipple, 1974).

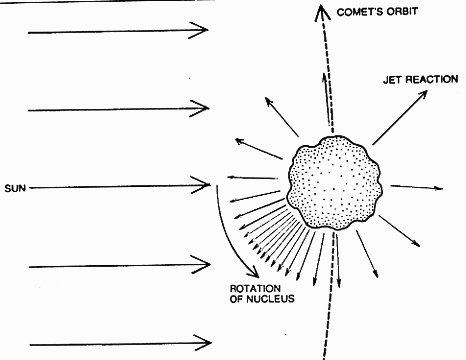
There is a division of opinion on the ejection of matter to produce nongravitational forces. Two schools exist, and their respective suppositions are:

(i) matter is ejected impulsively, especially at or near perihelion;
(ii) matter is expelled by the sublimation of surface ices in an essentially continuous matter (Marsden, 1968)

One should take note of the diference between the origin of comets and the mechanism by which they are observable in the inner regions of the solar system.

There is dissension on the subject of the origin of comets, dividing astronomers into two camps:

(i) those believing comets originated with or as an offshoot of the solar system;
(ii) those believing the origin of comets is in the interstellar clouds of dust and gas.

Wherever the comets originate, the puzzle to be solved yet is how they are brought to the inner regions of the solar system, where they may be observed. Given that the age of the solar system is in the vicinty of 4.5 x 10⁹ years, any solution of the problem must be able to account for the currently observed comets.

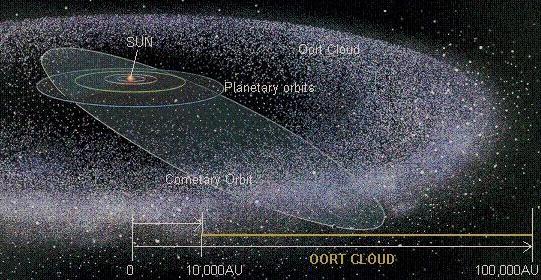
One possibility is that after formation comets are stored in vast numbers at the extremes of the solar system. The cloud of comets thus formed has become known as the "Oort cloud" and is fairly widely accepted as likely to exist. It is considered probable that perturbations of some description are responsible for bringing long-period comets from the Oort cloud region to the inner solar system.

However, there is contention over what type of perturbation is responsible for shifting comets out of their stable Oort cloud orbits. Three alternatives have been proposed as the source of such perturbations:

(i) the major planets, particularly Jupiter;
(ii) the nearby stars;
(iii) the galactic nucleus

2 - THE SOURCE OF COMETS

Three distinct hypotheses on the source of the presently observed comets exist. They may be characterised as:

(i) the 'eruptive' hypothesis
(ii) the 'interstellar' hypothesis
(iii) the 'Oort cloud' hypothesis

The Eruptive Hypothesis

The eruptive hypothesis proposes that comets are the product of volcanic eruptions on Jupiter and perhaps Saturn, Uranus, Neptune, or Jupiter's satellites. The idea was first suggested in 1814 by Lagrange, taken up later by Proctor in 1884 and Crammelin in 1910 and is today epoused by Vsekhsviatskii.

Veskhsviatskii (1977) gives the following as support for the hypothesis:

(a) the separation of cometary families from the different giant planets;
(b) the close approach of new short-period comets to Jupiter's system just prior to discovery;
(c) the existence of ices in the comet nuclei;
(d) the irregular shape of asteroids;
(e) the chemistry and structure of meteorites;
(f) the display of activity on the surfaces of planets and satellites;
(g) the existence of rings around Saturn and Uranus.

Judging that a total of 10¹⁵-10¹⁶ comets have been formed in the lifetime of the solar system, Vsekhsviatskii concludes that the mass loss from the solar system per annum is at least 10¹⁵g (1972) and probably near 10²⁰g (1977). He suggests that the same order of magnitude is lost in gas and dust in comet tails per year.

Various groups of short-period comets have been assigned to 'families' of the major planets. The theory behind such designations is that short-period comets tend to become trapped around one or other of the major planets because of the large planetary perturbations existing in those regions. Everhart (1969) made a study of the interaction of 10⁹ hypothetical random parabolic comets with the solar system. He examined the distributions which formed as a result of close-planet encounters.

Everhart makes the point that placing a comet in 'Jupiter's family', for example, makes the implicit assumption that an encounter with the planet will produce a characteristic period. His study revealed no evidence for such conclusions; unfortunately every one of Everhart's calculated distributions is in serious disagreement with the observed distribution.

Vsekhsviatskii concludes that there must exist a ring of comets and meteorites around Jupiter. Planetary perturbations of this ring eject individual comets into the inner solar system. It is deduced that the attendant rings of Saturn and Uranus demonstrate recent powerfully eruptive processes on those planets. Further, the presence of an atmosphere on Titan and Triton was discovered by G. P. Kuiper in 1947 and suggests the existence of inner heat source, implying volcanic activities.

Thus, Vsekhsviatskii maintains that all comets originate from volcanic activity on either the giant planets or other satellites. Long-period comets are those sufficienetly perturned by the planets to be edged into elliptical or nearly-parabolic orbits.

However, the eruptive hypothesis is not the complete answer: several problems are presented below.

Problems with an Eruptive Source

(a) Volcanic ejection from the surfaces of the giant planets would require very high velocities: for Jupiter, 67 km/s; for Saturn, 42 km/s (Lancaster-Brown, 1964);

It is possible that short-period comets may be 'born' with retrograde motion. In contrast, Jupiter's family of comets possesses direct motion.

Vsekhsviatskii (1962) proposed to eliminate both problems mentioned above by supposing that the satellites of the giant planets are the source of comets. In that case ejection velocities of the order of 1 - 7 km/s are required.

(c) While the eruptive hypothesis may provide some explanation of the origin of short-period comets, it offers little substantial evidence for the origin of long-period comets.

The Interstellar Hypothesis

There are two theories within the basic idea of an interstellar source:

(a) Lyttleton's 1953 accretion theory;
(b) Witkowski's 1972 theory of perturbation of interstellar comets.

Gething (1951) examined the early form of Lyttleton's hypothesis. Lyttleton (1948) suggested comets form during passage of the Sun through an interstellar cloud. In the solar gravitational field particles stream towards the axis of the Sun's motion. An accretion will form on the axis provided that the probability of collisions between particles is sufficiently high. Disruption of the accretion into relatively short line elements then produces potential comet nuclei.

However, such material would fall directly into the Sun. Lyttleton suggested that some of the nuclei formed might acquire angular momenta, falling into periodic orbits. He proposed two mechanisms which might produce the desired effect:

(a) the combined gravitational fields of the planets (planetary deflection);
(b) the gravitational effects of other stars (stellar deflection).

Witkowski (1972) maintains that comets exist ready-made in interstellar space. If the comets pass into the Sun's sphere of action they may be captured. Since the motion of interstellar gas and dust in the vicinity of the Sun depends on the galactic gravitational field, Witkowski proposes that the gas and dust should follow the motion of the stars in that region. That is, there should be a reflection of the phenomenon of star-streaming; Witkowski uses the term 'comet-streaming'.

An estimate of the Sun's sphere of action can be made according to Laplace's definition. Given that the Sun is 10⁴ parsecs from the galactic centre, possessing a velocity of 285 km/s and that the mass of the Galaxy is 1.9 x 10¹¹ times the mass of the Sun, Witkowski found the radius of the Sun's sphere of action to be 6.0 x 10⁴ AU. He also calculated the total number of 'cosmic' comets in the Galaxy as about 5 x 10²²,

Radzievskii and Tomanov (1987) have been recent vociferous proponents of the interstellar hypothesis. Their results suggest that short-period comets evolve from long-period comets acted on by perturbations.

Sekanina (1976) considered the problem of an encounter of the Sun with a cloud of interstellar comets. He concluded that the overwhelming majority of such comets would have strongly hyperbolic orbits, with 1/a < -0.1 (AU)^-1. The strongly hyperbolic comets were assumed to travel as part of a cloud with an appreciable velocity relative to the Sun (> 10 km/s) and a dispersion of individual velocities of at least 5 km/s.

Problems with an Interstellar Source

(a) Gething's theory of density asymmetries does not satisfactorily repair Lyttleton's accretion model: it is still unable to account for the existence of long and very long-period comets.

(b) The deviation of a strongly hyperbolic orbit from a parabolic one would be at least three orders of magnitude greater than the actual deviation of the most hyperbolic comet observed.

Sekanina suggests an alternative to overcome the problem of a manifest lack of observed strongly hyperbolic comets. If the cloud travelled wih the Sun, having zero systematic velocity and a very low dispersion of individual velocities ( <1 km/s), it would be expected that most of the "interstellar" comets would have nearly parabolic orbits. A few could possess slightly hyperbolic orbits. However, the aphelion distribution would be essentially isotropic.

(c) The distinct systematic motion of such a cloud of interstellar comets implies that there would exist a preferential direction in the distribution of cometary aphelia.

While there are authors who have concluded that such an anisotropy exists, the nature of the anisotropy is in some dispute. For example, Tyror (1957), Hurnik (1959) and Tomanov (1976) are in disagreement with Bailey (1977).

The existence of weakly hyperbolic orbits could be explained as a result of nongravitational perturbations of comets from a cloud of "interstellar" comets with zero systematic velocity relative to the Sun, but at this point the division between "interstellar" and "belonging to the solar system" becomes unclear. Bodies which exhibit the same motion as the Sun are considered to "belong" to the solar system. Sekanina's cloud with zero relative velocity will travel about the Galaxy with the Sun and in that sense is part of the solar system. It is only the origin of the comets within the cloud which is interstellar.

Like the eruptive hypothesis, the hypothesis of interstellar capture fails to account well for the observed distribution of comets. The last theory to be discussed is also the most widely accepted.

The Oort Cloud Hypothesis

Although the idea of a vast cloud of comets surrounding the solar system at great distances is an old one, J. H. Oort restated the idea in 1950 providing some correlation with facts of observation. He may be considered as the first to give the concept any link between theory and observation.

Oort proposed that "new" long-period comets come from distances of 0.5 - 1.5 x 10⁵ AU. The total number of comets in the cloud was estimated as about 10¹¹, constituting a total mass of the order of 0.01 - 0.1 times the mass of the Earth.

The observational evidence offered by Oort concerns the reciprocal semi-major axis, 1/a. Calculation of the distribution of original semi-major axes, 1/a_o, shows a marked peak at small values of 1/a_o. Of the 19 long-period comets, 10 had 1/a_o < 50 x 10^-6 AU^-1, and 4 had 1/a_o in the range of 50 - 100 x 10^-6 AU^-1. Each of the next 50 x 10^-6 AU^-1 bands contained one comet only.

Since Oort's 1950 sample included only 19 comets, Marsden (1977) extended Oort's data set to include 99 long-period comets for which accurate orbits were known. Marsden's results support those of Oort: the distribution of 1/a_o of long-period comets shows a steep increase at small values of 1/a_o; 58% of 1/a_o < 100 x 10^-6 AU^-1

The major planets exert considerable influence on the 1/a_o values; about half the comets of small 1/a_o values attain hyperbolic trajectates and as a result leave the solar system. The average change in 1/a, Δ, in those comets remaining in the solar system is approximately Δ = 500 x 10^-6 AU^-1, From this Oort drew the conclusion that since almost all the comets in his data set had 1/a_o < Δ, those comets were being observed on their first passage near the Sun.

To account for the large numbers of comets with small 1/a_o Oort proposed that the comets had been thrown from originally cicular orbits into nearly parabolic orbits of small perihelion distance. These perturbations were induced by the gravitational attraction of passing stars. Oort concluded that the effect of the combined actions of several distant stars would be less than that of a single relatively close passage.

Stellar perturbations have two effects on a cometary orbit:

(a) the semi-major axis a is slightly reduced
(b) the perihelion distance q is drastically reduced.

Having provided an explanation for the existence of long- and very long-period comets, the Oort cloud concept has been used by Kazimirchak-Polonskay (1972) to explain the existence of short-period comets. In her opinion there are three stages in comets' lifetimes after formation:

(a) accumulation in the Oort cloud;
(b) stellar perturbation of orbits;
(c) diffusion further into the inner solar system under the action of planetary perturbations.

(d) capture by the major planets into 'families'.

Bailey (1977) made a recent comprehensive study of the Oort cloud. He concluded that although the basic idea of a comet cloud was consistent with observation, the 1950 model requires considerable modification to be correct. The improved model suggeted by Bailey is smaller and flattened in the galactic plane, with an outer limit at 1.0 x 10⁵ AU.

Problems with the Oort Cloud

(i) Bailey questions whether all these long-period comets classed as 'new' by Oort are in fact on their first passage, since a small fraction of 'new' comets may return a second time to the Oort cloud vicinity. If the significant stellar perturbations are those of single close encounters, the returning comets may not experience another radical orbital change. The next passage could once again suggest a small 1/a_o value, implying 'newness' by Oort's criterion.

It must be kept in mind that only comets of perihelion distance ≤ 5 AU are observable on Earth. Thus it is possible that there exist numbers of unobserved short- and long-period comets.

(ii) The distribution of aphelion points in the cloud is subject to opinion. Bailey expects that the distribution be slightly anisotropic, but predicts a different concentration than those who espouse the 'galactic equator' concentration.

(iii)Were there past stellar encounters capable of perturbing the comets observed at present?

This last problem is by far the most significant one for the Oort cloud as the principal source of observed comets. To determine whether stellar perturbations of the appropriate type did occur, the author undertook a search of the Royal Observatory Annals (Woolley et al, 1970). Makover (1964) also made a star catalogue search with simlar intentions, but a different method.

The method used by the author may be characterised as a 'direct' method, since it depends on the star's proper motion and radial velocity. In contrast, Makover's method depends on the star's position and velocity components U, V, W.

3 - THE DIRECT METHOD

Stellar perturbations of the Oort cloud seem to be widely accepted in theory as the source of new comets. It remains to be seen whether the stars surrounding the solar system are capable of exerting such perturbations.

A computer search was therefore undertaken. The primary reference used was the Royal Observatory Annals (ROA). Anderson (1969) was used as a check for stars of very large proper motion.

The quantities of significance are the impact parameter (smallest Sun-star separation) and the time of closest encounter. The direct method uses the star's parallax π, proper motion μ, and radial velocity RV. Consider the diagram in figure 6.

Figure 6: Star with positive radial velocity RV.
Earth-Sun distance exaggerated for clarity.

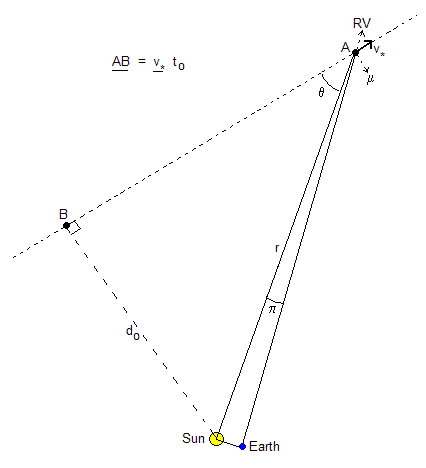
The time at which the star was observed is arbitrarily taken as t=0. At some time t_o the star will be at its point of closest approach to the Sun; there are three cases to note:

(i) t_o < 0 - the star made its closest approach some time in the past;
(ii) t_o = t = 0 - the star is at present at its closest to the Sun;
(iii) t_o > 0 - the star will reach its point of closest encounter with the Sun at some future time (see figure 7).

Figure 7: Star with negative radial velocity RV.
Earth-Sun distance exaggerated for clarity.

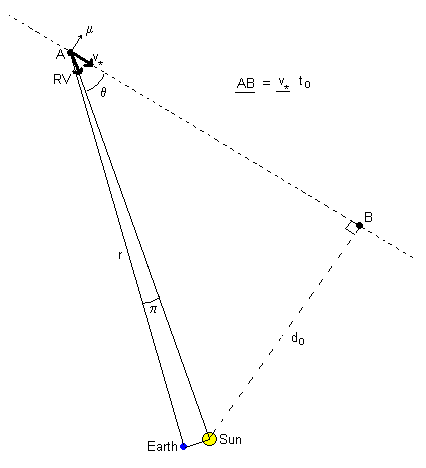
Let r be the distance of the star from the Sun at time t_o. The parallax is used to find r in parsecs

r = 1 / π

r = 206265 / π

v_μ = k r_e μ / π

1 AU = 1.488 x 10⁶ km
1 year = 3.156 X 10⁷ s
then k = 4.738 km yr / (s AU)

v_μ = 4.738 μ / π

v_* = [ (RV)² + (v_μ)²]^½

tan θ = v_μ / RV

(i) the parameters characterising the star's position, proper motion and velocity as given in the data sources are constant;

(ii) over sufficiently small time intervals, the star moves in a straight line.

These assumptions allow first-order estimates of the required quantities. However, there are limitations to the validity of the assumptions. For example, as a star draws closer to the Sun, its parallax will increases. The accuracy of the straight-line approximation depends on the "smallness" of the time interval. One criterion of "smallness" of a time interval,Δt say, is that

Δt << T

The Sun has a velocity of approximately 250 km/s relative to the centre of the Galaxy, corresponding to T = 2.3 x 10⁸ years. Thus Δt = 10⁶ years should be a sufficiently small time interval.

The impact parameter d_o is defined as the shortest Sun-star separation. A line drawn from the point of closest approach (B) to the Sun is then perpendicular to the star's velocity v_*.

Thus d_o is related to r, θ and v_* by

d_o = r | sin θ |

The time t_o of closest approach is determined using

t_o = - 4.738 r cos θ / v_*

Summarising, given a star's parallax, proper motion and radial velocity, the direct method enables calculation of the impact parameter and time of closest approach.

The Royal Observatory Annals were used as a data reference. The direct method was incorporated into a FORTRAN computer program run on the University of Newcastle RSTS system. The program is given in the Appendix.

Results

The results of the direct method search using the Royal Observatory Annals (ROA) are presented below in Table 3.1.

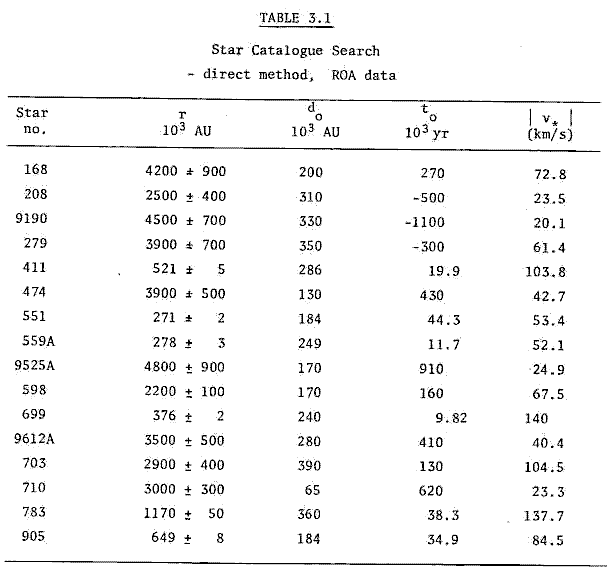
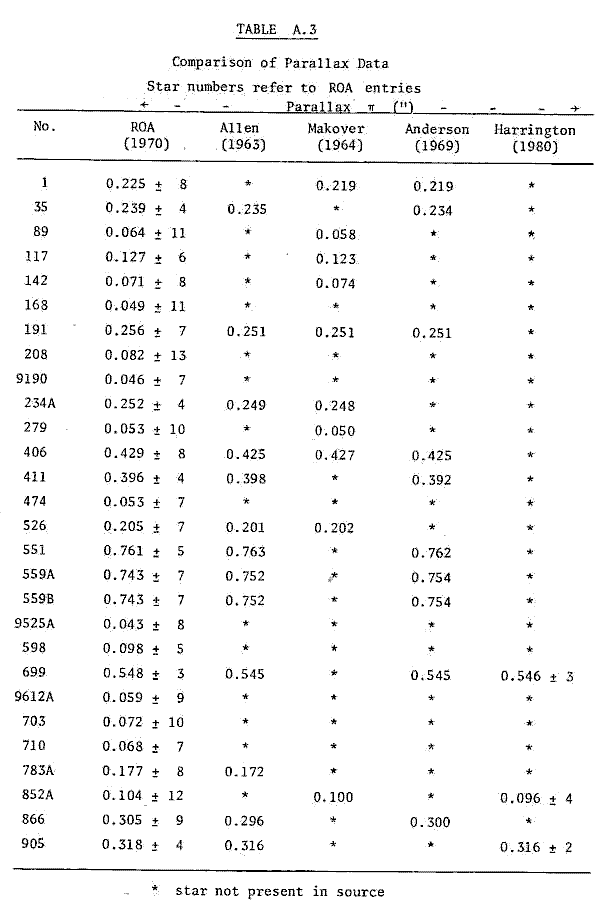
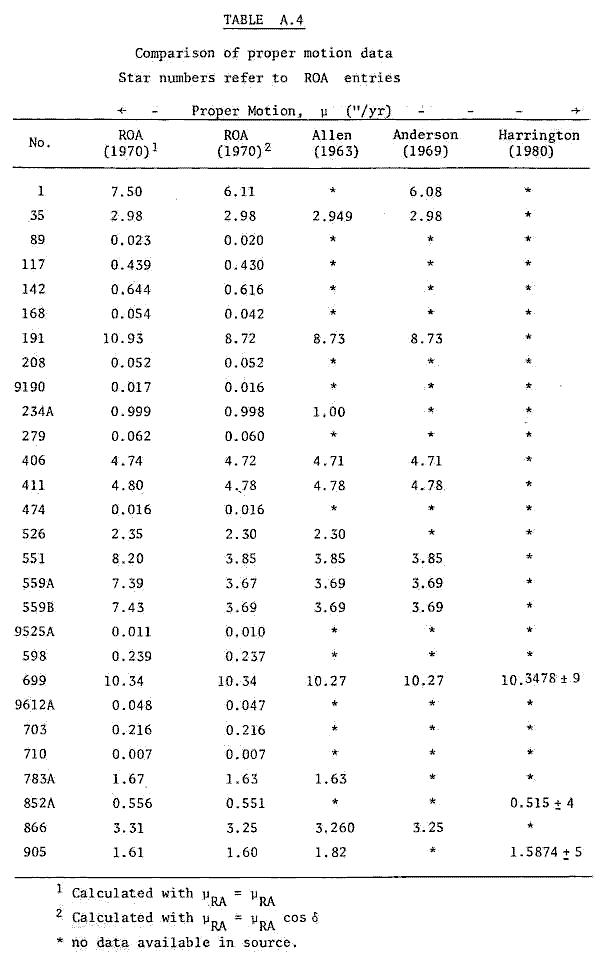
The first computer search using the direct method was made with μ_RA = μ_RA. Since Vorontsov-Vel'yaminov et al (1969) suggested that μ_RA was "often replaced" by μ_RAcos δ, a second computer search was made. The results in the above table are the results of that search. (See Table A.4 in the Appendix for a comparison of proper motion data. Stars with high μ_RA and δ show marked differences. To obtain data which were most consistent with the other sources available, μ_RA = μ_RA cos δ was adopted as a rule.)

The computer results are output only when the impact parameter is less than 4.0 x 10⁵ AU. If the Sun is not unique in possessing an accompanying comet cloud, other stars may possess such clouds. If such stars come close to the Sun, the possibility of 'mutual exchange' of protocomets from the extremes of the comet clouds exists. The upper limit was chosen to allow for that possibility. The data on the stars in the above table are tabulated in the Appendix, Table A.1.

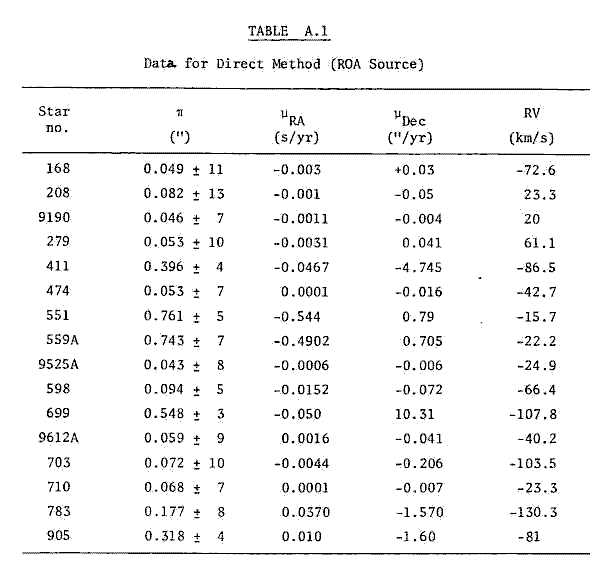
Anderson's 1969 data on stars of very large proper motion were also used. The program used was essentially the same as that for the ROA data, with modification for the different form of proper motion data. The Appendix contains the program (STARAN.FOR) and the results of this program are shown below. The selection criterion was again d_o ≤ 4.0 x 10⁵ AU.

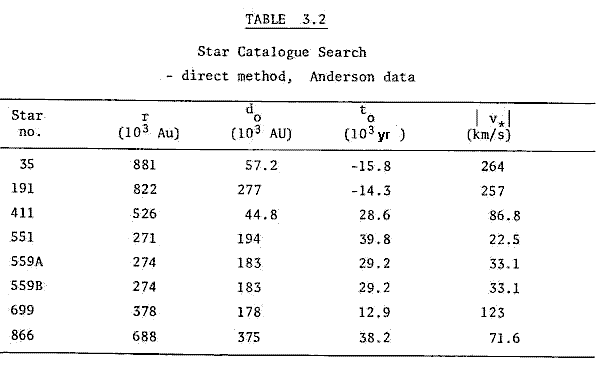
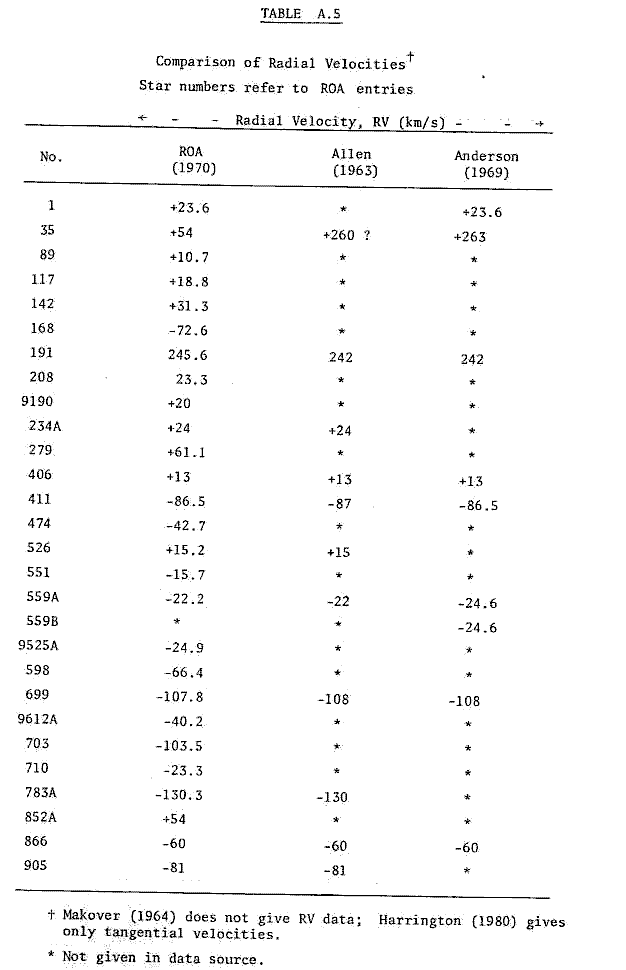
Comparisons of the two tables reveals that stars 411, 551, 559A and 699 are common to both. While the results for 551 (Proxima Centauri) and 699 (Barnard's star) are in good agreement, stars 411 (Lalande 21185) and 559A (α Centauri A) show discrepancies. Inspection of the data comparison tables in the Appendix (Tables A.3, A.4 and A.5) shows that data on 559A differs significantly in parallax, proper motion and radial velocity. Star 411 also shows differences in proper motion.

Star no. 35 has a dubious radial velocity. The value used by Anderson (263 km/s) was rejected by Woolley (1970) in compiling th ROA. Stars no. 191 and 866 do not appear in Table 3.1. This is a result of the earlier adoption of μ_RA = μ_RA. If μ_RA cos δ is used instead, these stars would seem to have d_o ≤ 4 x 10⁵ AU.

The earliest form of the data file used in DIRECT.FOR included only star number, parallax, proper motion and radial velocity. It is therefore possible that the search may have 'missed' stars likely to approach the Sun at distances ≤ 4 x 10⁵ AU as a result of not taking the cos δ factor into account.

The results of the direct method (ROA) search suggest that star no. 208 came as close as ~ 3.10 x 10⁵ AU some 5.0 x 10⁵ years ago. The next closest encounter was that of star no. 9190 (ζ Lep) at a distance of ~ 3.30 x 10⁵ AU about 1.10 x 10⁶ years ago. The only other past stellar encounter found was that of star no. 279 at a distance of ~3.5 x 10⁵ AU about 5 x 10⁵ years ago.

The direct method (ROA) search indicated that the closest future encounter to be expected is that of star no. 710 at only 6.5 x 10⁴ AU in only 6.5 x 10⁴ years' time. The next closest future encounter is that of star no. 474, which will be 1.3 x 10⁵ AU distant in ~4.30 x 10⁵ years' time.

4 - MAKOVER'S METHOD (1964)

S. G. Makover proposed to search Gliese's (1957) star catalogue to find whether there were stars which had passed close to the Sun in the past. The method he used follows (see figure 8).

Figure 8: Simplified diagram of star's position and velocity components.

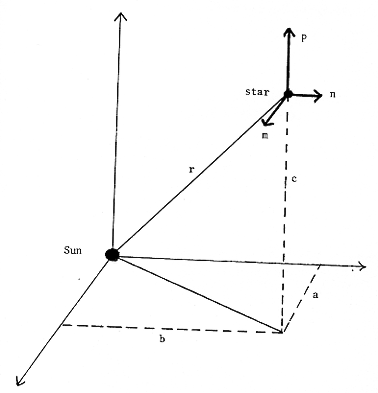
The units of distance and time were taken as 10⁴ AU and 10⁴ years respectively. A star with parallax π (in seconds of arc) is at a distance of r from the Sun, where

r = 206265 x 10^-4 / π

(i) the right ascension α (in hours, minutes and seconds)
(ii) the declination δ (in degrees and minutes of arc).

a = r cos δ cos α
b = r cod δ sin α
c = r sin δ

 ( m )   ( 0.0206 -0.1022 -0.1835 ) (  U )
 ( n ) = ( 0.1853  0.0955 -0.0324 ) ( -V )
 ( p )   ( 0.0987 -0.1580  0.0991 ) (  W )

t_o = - (am + bn + cp)/(m² + n² + p²)

Δa = m t_o
Δb = n t_o
Δc = p t_o

d_o² = [(a + δa)² + (b + δb)² + (c + δc)²]
or
d_o² = (a² + b² + c²) + (am + bn + cp) t_o

(i) parallax π
(ii) right ascension α and declination δ
(iii) components of speed U, V and W.

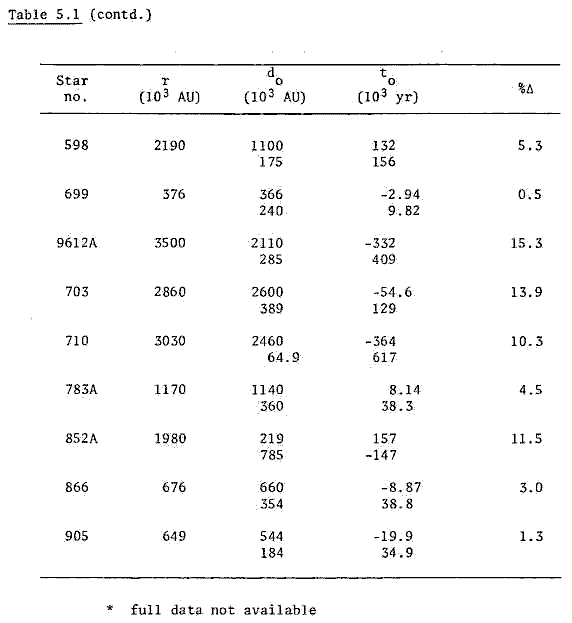
Makover used Gliese (1957) as a data source. Since that source was unavailable to the author at the time of writing, it was not possible to check Makoever's results using the original data source. It was possible to check his method using the data of the Royal Observatory Annals, which used Gliese's numbering system with addition of stars up to 25 parsecs from the Sun.

Makover's method was incorporated into a FORTRAN program, MAKOVER.FOR . The selection criterion d_o ≤ 4 x 10⁵ AU was again applied to eliminate all but 'close' encounters. The results of that computer search are set out in the table below.

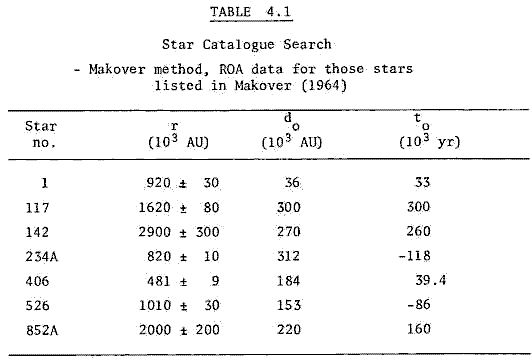
Table 4.2 contains the results of Makover (1964) for those stars listed in Table 4.1. Comparison of Tables 4.1 and 4.2 indicates that the present distances, r, are in good agreement. However that is not the case with impact parameters d_o and times of closest encounter, t_o. The only star that has the right order of magnitude and the right sign for d_o and t_o is 234A (Ross 614).

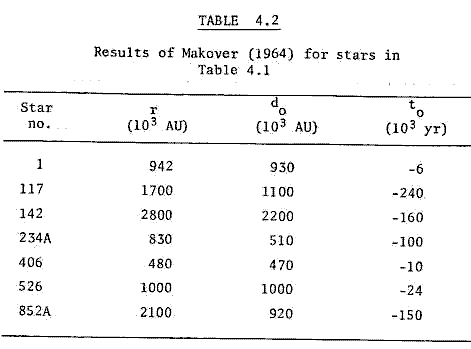
One explanation for this disagreement may lie in the different data sets. While the parallax data compare well (see Appendix, Table A.3), there may be other differences in the Gliese and ROA catalogues. A total of five sources of data were available: besides the ROA (1970) and Anderson (1969) sources mentioned earlier, Makover gave some data (1964). The other sources available were those of Allen (1963) and Harrington & Dahn (1980).

The data sources were used to compare parallax, proper motion and radial velocity for any star found as a result of any search. The comparisons are tabulated respectively in Tables A.3, A.4 and A.5 in the Appendix. Unfortunately the ROA is the only source containing U, V, W data, so no comparison of such data is available.

It is possible that the galactic components U, V and W are a significant source of differences in data, since they are calculated from parallax, proper motion and radial data.

One discrepancy in the data sets is not apparent from the table. Stars no. 344, 470 and 600 have no U,V,W components given in the ROA, presumably because they are now too distant. (Their parallaxes are given respectively as 0.037", 0.015", and 0.036"; these should be compared with 0.052", 0.057" and 0.055" given in Makover (1964).)

The advantage and disadvantage of both the direct and Makoever methods will be discussed in Chapter 5.

The results of applying Makover's method to the ROA data indicate that the star no.526 (Wolf 498) passed closest to the Sun some 8.6 x 10⁴ years ago with an impact parameter of 1.53 x 10⁵ AU. The next closest encounter was that of star no.234A (Ross 614) at a distance of 3.12 x 10⁵ AU some 1.18 x 10⁵ years ago.

The closest future encounter is likely to be that of star no.1 (LFT 5) with an impact parameter of 3.6 x 10⁴ AU some 3.3 x 10⁴ years hence. Star no.406 will come next closest, with an impact parameter of 1.84 x 10⁵ AU in about 3.94 x 10⁴ years' time.

5 - COMPARISON OF DIRECT AND MAKOVER METHODS

Having devised a method to calculate impact parameters and times of closest approach, the next step was to compare that method with an alternate one. Both methods were used, as previously outlined, and were coded in separate FORTRAN programs.

To compare the methods the program COMPAR.FOR was written (see Appendix), The output of COMPAR gives present distance, impact parameter, time of closest approach and percentage uncertainty in the present distance due to parallax uncertainty. Since both methods depend heavily on parallax the percentage uncertainty should be considered a minimum estimate in the other quantities.

Altogether the methods have indicated some 26 stars as likely to approach the Sun at distances ≤ 4 x 10⁵. The data of the ROA are used for reference in COMPAR.FOR, that source being the most comprehensive available at the time. The results of COMPAR.FOR are set out in Table 5.1 below.

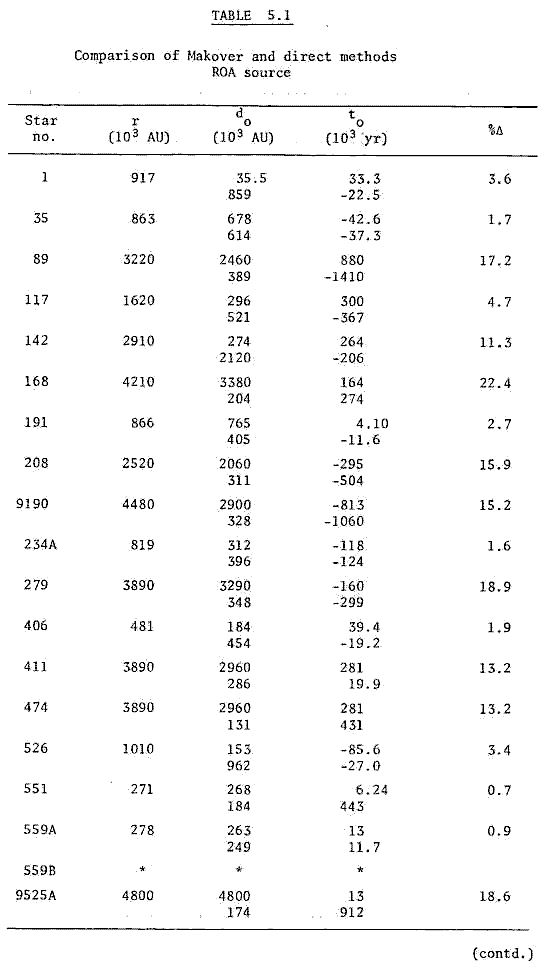
The results of the program COMPAR.FOR reveal that of 293 stars contained in the data file MAKOVR.DAT (those stars listed in Makover 1964), 77 stars have d_o and t_o results which agree in order of magnitude and sign of t_o. This represents 26% of the total. Without Makover's data source (Gliesse, 1957) it is not possible to assert that the two methods are completely equivalent. It would appear that for 26% of the stars the methods are equivalent: one would need to examine the data to determine whether stellar characteristics mean the methods are equivalent (for example, low radial velocities, small parallax or small proper motion).

If the two methods are equivalent, it can be demonstrated that the direct method is simpler and more efficient. In terms of data for a particular star, the direct method requires only three quantities:

1. parallax
2. proper motion
3. radial velocity

In contrast Makover's method requires six quantities:

1. right ascension and declination
2. parallax
3. components of galactic velocity U, V, W

There is another distinction between the methods. Makover's method locates the star in three-dimensional space (see figure 8), using three linear components to calculate d_o and t_o.

However, the important feature of the problem is the star's distance. At this stage the star's spatial coordinates are of no particular significance, although they could become important for an asymmetric Oort cloud. The two points of interest are the Sun and the star: the resultant of the proper motion and the radial velocity vectors defines a star's velocity vector. This vector and the two points define a plane, so the direct method treats the situation as two-dimensional.

6 - CONCLUSIONS AND SUGGESTIONS

Conclusions

The direct method search found that in the past, the closest impact parameters of stars were of the order of ~3 x 10⁵ AU; the times of these encounters were ~4-11 x 10⁵ years ago.

The search using Makover's method found the past closest encounters occurred at distances of ~1.5-3.0 x 10⁵ AU approximately 1.0 x 10⁵ years ago. The direct method search suggest that future closest encounters can be expected in ~4 - 6x10⁵ years' time; the closest encounter will be at 6.5 x 10⁴ AU and the next closest at ~1.3 x 10⁵ AU. The results of the search via the Makover method predict closest future encounter in 3-4 x 10⁴ years' time; the closest encounter will be ~4 x 10⁴ AU. The next closest will be at ~2 x 10⁵ AU.

The direct method results have the right order of magnitude in time to perturb the Oort cloud and thus produce the presently observed comets. Unfortunately the impact parameters are ~1.5 times the maximum radius assumed for the Oort cloud: although relatively "close", it is unlikely that they are close enough to provide the requisite stellar perturbations.

Makover's method yields results which may be more suitable in terms of impact parameter, but are perhaps low in order of magnitude of time.

It must be concluded that the computer search undertaken does not provide definitive evidence to support the hypothesis that close stellar perturbations of the Oort cloud provide the presently-observed comets.

The results obtained are necessarily only first-order estimates. Refinement of the method(s) should incorporate these 'initial values'. Only then can some 'experimental' weight be placed behind any hypothesis using 'theoretical' stars.

Suggestions for Further Research

The next stage for the direct method will be to include the factor cos δ in the determination of proper motion for all the ROA data. Although it is not expected that this step will greatly increase the number of close-approaching stars found, it will at least allow for the stars with high μ_RA and declination which escaped notice in the earlier programs.

It would have been useful to have the entire contents of the Royal Observatory Annals stored permanently on Dectape, for instance. Fast access to the catolgue information would then be possible. As the ROA were the most comprehensive data reference available, storing other references (eg Gliese 1957, Allen 1963, Anderson 1969, Harrington & Dahn 1980) would take second priority until a reference as comprehensive is available. If the time and space were availble other data sources would be handy to use in comparison.

To check Makover's method the Gliese (1957) catalogue should be used. This would allow the method and results given in Makover (1964) to be compared with results of the application in 1980 of Makoever's method to the ROA data. If then the two methods are inconsistent, the problem will be to determine which method (if either) is applicable to the problem.

If the two methods are consistent, or if either method is shown to be valid within certain limitations, the stars found to approach the Sun closely should be analysed for their possible effects on comet orbits. An appropriate method is to be found in Rickman (1976).

If such analysis indicates that certain stars did pass close enough to the Sun at some time in the past, the next step would be to determine whether such stellar encounters could be responsible for the perturbations of the proto-comets supposed to exist in the Oort cloud.

On the other hand, there may be no stars found to produce the Oort cloud perturbations. In that case one is faced with two alternatives:

(i) the data available is insufficient;
(ii) the hypothesis of stellar perturbations of the Oort cloud is invalid.

It may be that a rapidly moving star did approach the solar system in the past, perturb the Oort cloud proto-comets sufficiently and move on out of the vicinity of the Sun. In such a case the straight-line approximation methods are useful only to provide first-order estimates. It may then be necessary to investigate whether the technique of box-orbit computation would improve results (Woolley, 1970).

The second alternative can only be considered after exhaustive checking of the first. It may be the concept of the Oort cloud may require revision in shape and size for instance. Further work along these lines could investigate the effects of the known stellar encounters on various models of such a proto-comet cloud.

Modification of the origin of the Oort cloud may be required; van Flandern (1978) proposes a former asteroidal planet as the origin of proto-comets which are stored in the Oort cloud. Sekanina (1976) has suggested that a cloud of interstellar comets with zero systematic velocity may perhaps accompany the Sun and give rise to the presently observed comets.

Kresak (1977) sees the Oort cloud not as a source of comets, but as a region of 'rejuvenation' of old comets. This idea is not without difficulties. The diffusing effect of planetary perturbations would tend to cause degeneration of long-period comets into short-period orbits. The actual mechanism by which the comets returning to the Oort cloud region are replenished is not outlined clearly.

Nezhinskii (1972) attempted to estimate the rate of destruction of the Oort cloud by stellar passages. A lower limit of 1.1 x 10⁹ yr was estimated for the cloud's half-life. Such numerical estimates also indicated that the dominant effects are those of cumulative passages. The methods outlined in this report may possibly be used to correlate Nezhinskii's estimates with the known passages. For example, Nezhinskii states that the cloud density will be decreased by half by the passage of 5.5 x 10⁴ stars through the cloud in 8.6 x 10⁹ years.

Wyatt and Faintich (1971) have considered the effects of various galactic objects in removing comets from the outer limits of the Oort cloud. The combined effect of interstellar clouds and stars may need to be examined. Weissman (1977) used Monte Carlo methods to determine the random scattering of comets due to perturbations by star and interstellar clouds. His model is in agreement with the suggestions made by Wyatt and Faintich. Weissman also found that the summed stellar perturbations were capable of causing radical changes in original cometary orbits.

In summary, continued examination of stellar data will allow critical appraisal of the various hypotheses of comet sources. In particular, evidence for or against the theory of stellar perturbations of the Oort cloud will be provided.

Quite apart from its consequences for the Oort cloud, the analysis of stellar motions should refine and expand the state of knowledge of stars presently in the vicinty of the Sun.

REFERENCES

Allen, C.W., 1963, Astrophysical Quantities, Great Britain: The Althone Press, University of London, (2/e).

Anderson, J.H., 1969, "The Stars of Very Large Proper Motion", Sky & Telescope, (USA), Aug., pp1976-78.

Bailey, M.E., 1997, "Some Comments on the Oort Cloud", Astrophysics & Space Science, 50, pp3-22.

Chebotarev, G.A., 1972, "Evolution of Cometary Orbits on a Cosmogenic Time Scale", in IAU Symposium No.45, pp1-5.

Corlin, A., 1939, "On the Builing up of Larger Bodies from Small Particles in Interstellar Space", Z. Astrophys. (Germany), 18, pp1-24.

Dermott, S.F. & Gold, T., 1978, "On the Origin of the Oort Cloud", Astron J., (USA), 83, pp449-450.

Everhart, E., 1969, "Close Encounters of Comets and Planets", Astron J., (USA), 74, pp735-750.

Gething, P.J.D., 1951, "Accretion and Origin of Comets", Monthly Notices of the Royal Astronomical Society, (GB), 111, pp468-477.

Gingerich, O., 1975, New Frontiers in Astronomy, (Introductions), San Francisco: W.H. Freeman & Co..

Harrington, R.S. & Dahn, C.C., 1980, "Summary of U.S. Naval Observatory Parallaxes", Astron J., (USA), 85, pp454-465.

Hurnik, H., 1959, "The Distribution of the Direction of Perihelion Distance and of the Orbital Poles of Non-Periodic Comets", Acxta Astron., (Poland), 9, pp207-221.

Kazimirchak-Polonskaya, E.I., 1972, "The Major Planets as Powerful Transformers of Cometary Orbits", in IAU Symposium No. 45, pp373-397.

Kresak, L., 1977, "An Alternate Interpretation of the Oort Cloud of Comets?", in Comets, Asteroids, Meteorites: Interrelations, Evolution and Origins", Toledo: University of Toledo, pp93-97.

Lancaster-Brown, P., 1964, "A Review of the Current Theories of Origin and Formation of Comets", Journal of the British Astronomical Association, 75, pp17-29.

Lyttleton, R.A., 1948, "On the Origin of Comets", Monthly Notices of the Royal Astronomical Society, (GB), 108, pp465.

Makover, R.A., 1964, "On Perturbations of Comets by Stars". Byell, Inst. Teor. Astron., (Leningrad), 9, pp525-536.

Marsden, B.G., 1968, "Comets and Nongravitational Forces", Astron J., (USA), 73, pp367-379.

Marsden, B.G., 1977, "Orbital Data on the Existence of the Oort Cloud", in Comets, Asteroids, Meteorites: Interrelations, Evolution and Origins, Toledo: University of Toledo, pp93-97.

Nezhinskij, E.M., 1972, "On the Stabilty of the Oort Cloud", in IAU Symposium No.45, pp335-340.

Oort, J.H., 1950, "The Structure of the Cloud of Comets Surrounding the Solar System and a Hypothesis Concerning its Origin", Bull. Astron. Inst. Neth., (Netherlands), 11, pp91-110.

Radzievskii, V.V. & Tomanov, V.P., 1978 "Statistical Consequences of the Capture of Comets by the Laplace Scheme", Soviet Astronomy, (USA), 21, pp503-506.

Rickman, H., 1976, "Stellar Perturbations of Orbits of Long-Period Comets and their Significance for Cometary Captue", Bull. Astron. Inst. Czech., (Czechoslovakia), 27, pp92-105.

Sekanina, Z., 1976, A Probability of Encounter with Interstellar Comets and the Likelihood of their Existence", Icarus, (USA), 27, pp123-133.

Tomanov, V.P., "The Solar Apex Relative to the Protocometary Cloud", Soviet Astronomy, (USA), 20, pp366-370.

Tyror, J.G., 1957, "The Distribution of the Directions of the Perihelia of Long-Period Comets", Monthly Notices of the Royal Astronomical Society, (GB), 117, pp370-379.

van Flandern, T.C., 1978, "A Former Asteroidal Planet as the Origin of Comets", Icarus, (USA), 36, pp51-74.

Vorontsov-Vel'yaminov, B.A., 1969, Physics of Stars and Stellar Systems Volume 2 of A Course in Astrophysics and Stellar Astronomy A.A. Mikhailov (Ed.), Jerusalem: Israel Program for Scientific Translations.

Vsekhsviatskii, S.K., 1962, "Comets, Small Bodies and Problems of the Solar System", Publ. Astron. Soc. Pacific, (USA), 74, pp106-115.

Vsekhsviatskii, S.K., 1972, "The Origin and Evolution of the Comets and Other Small Bodies in the Solar System", in IAU Symposium No.45, pp413-418.

Vsekhsviatskii, S.K., 1977, "Comets and the Cosmogony of the Solar System", in Comets, Asteroids, Meteorites: Interrelations, Evolution and Origins, Toledo: University of Toledo, pp469-473.

Weissman, P.R., 1977 "Initial Energy and Perihelion Distributions of Oort-cloud Comets", in Comets, Asteroids, Meteorites: Interrelations, Evolution and Origins, Toledo: University of Toledo, pp87-91.

Whipple, F.L., 1950, "A Comet Model. 1. The Acceleration of Comet Encke", Astrohysics Journal, (USA), 111, pp375-394.

Whipple, F.L., 1974, "The Nature of Comets", in New Frontiersin Astronomy, San Francisco: W.H. Freeman & Co., pp36-45.

Witkowski, J.M., 1972, "On the Problem of the Origin of Comets", in IAU Symposium No.45, pp419-425.

Woolley, R., 1970, "Box Orbits of Nearby Stars", Volume II of Galactic Astronomy, Chiu, H-Y & Muriel A, (Eds), New York: Gordon & Breach, 1970, pp95-159.

Woolley, Sir R., Epps, E.A., Penston, M.J. & Pocock, S.B., Royal Observatory Annals Number 5, Catalogue of Stars within Twenty-Five Parsecs of the Sun, Herstmonceux: Royal Greenwich Observatory, 1970.

Wyatt, S.P. & Faintich, M.B., 1971, "The Effect of Interstellar Clouds on the Comet Cloud", Bulletin of the American Astronomical Society, (USA), 3, pp368+.

APPENDICES

COMPUTER PROGRAMS

The original thesis included code listings for the following programs:

STARS5.FOR - for processing ROA data by direct method
STARS5.RES - output file from STARS5.FOR
STARAN/STARS4.FOR - for processing Anderson data by direct method
STARS4.RES - output file from STARS4.FOR
MAKOVR.FOR - for processing ROA data by Makover method
COMPAR.FOR - for comparison of the data from the two methods

Unfortunately there is insufficient data in the thesis to reconstruct input files for the other programs. Those wishing to do so will need to consult the original references for this data.

Australian Space Academy