
INTRODUCTION
In his science fiction novel "The Black Cloud" Fred Hoyle introduces a mathematical concept that at first seems very strange. An astronomer finds a dark region on a photographic plate he has just exposed. A few days later another image is taken. The black 'object' is still there in the same place with respect to the stars, but it has increased in size.
The situation is illustrated by the two stellar images shown below:

Between the two observations the object has 'grown' by 20.5 arcseconds.
Now we only know the angular diameter of the object at the two times, We don't know its true size (diameter) and we don't know how fast it is travelling.
Despite this our intrepid astronomer calculates that the object will collide with the Earth in 10 days! (Hoyle even shows how to do this calculation as a footnote to the story!)
WILL THERE BE A COLLISION?
| The first question we should ask ourselves is "How do we know a collision is going to occur at all?" The situation is similar to one experienced in terrestrial aviation (shown at right). If the pilot of the fast plane has a constant bearing to the plane on his right, then he knows that a collision will occur, and he must change his direction and/or altitude. If the bearing angle Bc increases with time, the fast plane will arrive at the point X before the slow plane and he will pass in front without a collision. If the bearing angle decreases with time the slow plane will arrive at the point X before the fast plane and again there will be no collision. However, if the bearing angle is constant, the pilots know that a collision is certain, despite not knowing the speed of the other aircraft and their distances to the intersection point. |
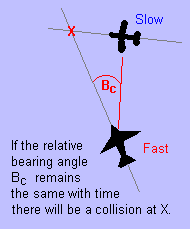
|
In the astronomical case the astronomer knows that a collision will occur because the object remains in the same place relative to the starry background. Of course, he has to assume that the instrinsic size of the object does not change with time, and that the object's velocity is also contant. That is, it travels in a straight line with constant speed.
Now in reality, the Earth and the other bodies in the solar system orbit around the Sun in elliptical orbits. Any visitor to the solar system would also be influenced by the Sun and would show some type of curve, even it is not an ellipse but rather a parabola or hyperbola. However, over short periods of time, a small section of the orbit will be close to a straight line. So even only a small shift in position between the two images would be cause for concern, for any object that showed significant growth in angular diameter.
COLLISIONAL MECHANICS
The geometry of the situation is shown below:
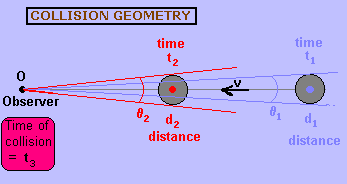
Let us denote the unknown instrinsic diameter of the object as 'a', and its unknown speed (relative to the Earth) as 'v'.
The only measurements we can make are apparent angular diameters θ1 at time t1 and θ2 at time t2. Let us designate the time between the two observations as Δto = t2 - t1. Furthermore let us designate the time between the second observations and the time of collision as Δtc = t3 - t2. This is the remaining time until collision occurs.
Now as long as the angle θ subtended by an object is not too large (ie less than a few degrees), we can use the relation {θ = object_diameter / object_distance}. Thus:
CALCULATION
For the above example we can substitute the values of time and subtended angles to give the time to collision:
 Australian Space Academy
Australian Space Academy