ROCKET

SCIENCE

 Rocket Science
(Image: Popular Mechanics)
INTRODUCTION

There is a public perception that the science related to rocketry is very difficult - hence the negative expression "it's not rocket science" said about something that is not difficult.

The truth is that the physical and mathematical foundations of rockets are not difficult, which we will attempt to show. What is difficult is not rocket science, but rocket engineering. The basic principles underlying rocket science were laid down by Isaac Newton. However, applying those principles to escape the Earth's gravity requires high pressures, temperatures and velocities, and finding materials and building structures to withstand these parameters is the really difficult part.

THE FOUNDATION LAW

The British scientist Isaac Newton stated three fundamental laws of mechanics that are very important in a number of disciplines, including rocketry. These laws are:

These laws are not intuitive, and in fact N1 seems to go against common experience. For example, when you throw a ball its velocity is constantly changing even after it leaves your hand that accelerated it to an initial velocity.

The resolution of this discrepancy is of course that on the Earth, the ball is contantly exposed to the external force of gravity (and to a lesser extent air resistance) and these forces determine its subsequent motion.

However, in space, well away from the influence of any massive body (such as a planet or a star) an object will continue to move at a constant velocity.

The third law (N3) is the basis of rocket motion. If we throw something out the back of a rocket, the rocket will move forward. You can demostrate this by holding a brick while standing at rest on a skate board on a horizontal surface. On throwing the brick in one direction, you will move off in the opposite direction. You will eventually come to rest again, but this is because of frictional forces acting on the board (and yourself).

It is the second law (N2) however that allows us to compute how much stuff we have to throw out the back of a rocket and how fast it needs to be thrown, for of the three laws N2 is a quantitative law that permits mathematical calculations.

Many high school students learn that Newton's second law may be written as the formula F = m a, where F is the external force on the body, m is its mass and a is its acceleration. However, if we applied this formula to rocketry where the external force is zero (at least in deep space), we would have to conclude that the acceleration of the rocket was zero - that is, a rocket could never work. However, this is obviously not so.

The resolution is that although in many practical situations (those in whch the mass of the body is constant) F=ma is quite adequate, Newton did not state N2 in this form. The reason that in rocketry, F=ma is totally inadequate, is due to the fact that the mass of the rocket is continually changing, as gases are shot out the back. The most general form of N2 may be written:

In the following sections we will see how this form of N2 can be applied to give us the mathematical foundations of rocket science.

Isaac Newton Isaac Newton (1643 - 1727) formulated the laws of physics relating to the motion of objects, and set the stage for quantitative rocket science. These laws were set forth in his book "Principia Mathematica Philisophiae Naturalis" published in 1687. Rocket

BRIEF HISTORY OF ROCKET SCIENCE

The history of the use of rockets may trace back into antiquity, and is certainly established in China in the 13th century. However, these uses are rocket engineering, on an experimental basis without an underlying basis of the relevant science. True rocket science is generally traced to the Russian high school mathematics teacher Tsiolkovsky who in 1903 published a work with a title translated as "The Exploration of Cosmic Space by Means of Reaction Devices". This work was virtually unknown outside Russia for many decades.

In America Robert Goddard started directed experimentation with rockets and published his ideas in a 1919 work entitled "A Method of Reaching Extreme Altitudes".

In Germany in 1923 Hermann Oberth published a version of his doctoral thesis "The Rocket into Planetary Space" after the thesis was rejected by the University of Munich.

Konstantin Tsiolkovsky
Konstantin Tsiolkovsky (1857-1935)		 Robert Goddard
Robert Goddard (1882-1943)

THE ROCKET EQUATION

When a rocket is used for propulsion in outer space, there are no external forces acting on it (we will consider the case of planetary operation later). Thus, in N2, we may write F=0. This then gives us the formula:

Now p = m v is a function of both the mass and velocity of the rocket, and both of these quantities will change with time. We thus need to differentiate the two variables with respect to time. That is: Now dv/dt = a , the acceleration of the rocket. Solving for 'a' we have: dm/dt is the change in the mass of the rocket with time, and as the rocket mass is decreasing, dm/dt will be negative, giving a positive acceleration in the forward direction. dm/dt at any instant is also the rate at which gases are being pushed out the back of the rocket. m is the instantaneous mass of the rocket is v is the velocity of the rocket exhaust gases with respect to the rocket, and we will henceforth write it as ve. In many cases we can assume ve is relatively constant.

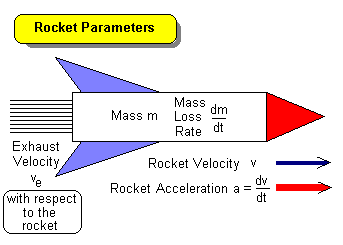
Rocket variables

Typical values of exhaust velocity are given for various chemical propellants in the table below.

Propellantsve m/s
Solid Fuel in Model Rocket 850
Solid Fuel - Large Boosters 2300
Oxygen - Kerosene 2500
Nitrogen Tetroxide - Hydrazine 2900
Oxygen - Ammonia 2900
Oxygen - Hydrogen 3600
Fluorine - Hydrogen 4000

To find the velocity of the rocket at any instant we must integrate the above equation with respect to time:

Note we have removed the exhaust velocity outside the right hand integral because it is assumed constant. If we substitute back a = dv/dt in the left hand integral: where vi and vf are the initial and final forward velocities of the rocket respectively, and mi and mf are the initial mass (at the start of the rocket burn) and final mass (at the end of the burn). The function ln( ) is the natural logarithm of the argument.

If we let Δv = vf - vi then the solution of the above equation gives us an expression for Δv, the increase in forward velocity of the rocket due to the burn:

This is called the "rocket equation". We will refer to it as R1, and it is presented graphically below.

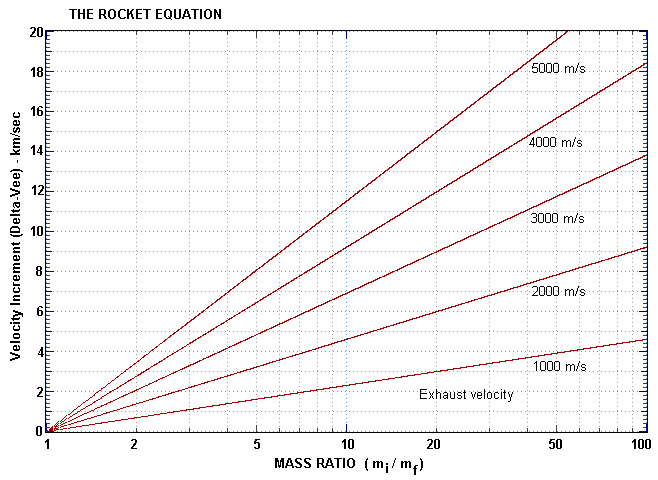
Rocket Equation Graph

In practice, liquid fuelled rockets have mass ratios below 10 whereas solid fuelled rockets may achieve mass ratios of up to 20.

We can turn R1 around to determine the required mass ratio (mi/mf) for a specified Δv :

It is sometimes useful to define the mass loss of the rocket as a fraction of the initial mass: Note that mi - mf is the mass of the fuel burnt (ie mfuel = mi - mf). ζ is then the ratio of the fuel mass to the total mass (of the fueled rocket): ζ = mfuel / mtotal.

A little bit of algebra gives us a third version of the rocket equation as a function of ζ (zeta) :

THE THRUST EQUATION

The rocket equation (R1) tells us that the change of velocity of a rocket due to a fuel 'burn' is only related to the exhaust velocity and the total amount of fuel consumed. It does not say anything about the duration of the burn. It is thus not the whole story, for time is very relevant when we need to consider the thrust of the rocket at any instant. This is something that is extremely important when trying to take off from a planetary surface where gravity is acting.

Consider the example of an ion drive where small sub-atomic particles are accelerated to very high velocity (ve) and thus result in a very efficient rocket engine. Because only a limited number of particles can be accelerated to high velocity every second, the thrust is small, and so although very efficient for travel in zero gravity conditions, an ion engine is useless to try and escape the gravitational pull of a planet.

The thrust equation results very simply from the application of N2 to the rocket:

The two terms in the expansion of the time derivative of momentum both have the units of force, and it is the second one that provides the thrust. Thus we can write that the thrust force on the rocket at any time is: The acceleration that the rocket will experience from this thrust in zero gravity will be (according to N2): where m is the mass of the rocket at the time the acceleration is calculated.

In a gravitationl field g (this is the acceleration due to gravity and has the units of metre per second squared), the total force acting on the rocket as it lifts off from the surface of the gravitating body (eg a planet) is:

where W = mg is the weight of the rocket (fully fuelled at liftoff). Note that the unit of mass is the kilogram but the scientific unit of weight is the Newton, the unit of force. Thus a mass of one kilogram has a weight of 1 x g Newton. At the Earth's surface g=9.8 m s-2 and so one kilogram weighs approximately 10 Newton (to within an accuracy of 2%). On the lunar surface one kilogram of butter weighs only 1.6 Newton (glunar ~ 1.6 m s-2), but you still have the same mass or amount of butter that you had on Earth and it will still go just as far when you spread it on toast.

The resultant initial acceleration of the rocket when the engines are first lit is thus:

To achieve a successful take off it is thus necessary that FT > W or that: For a large liquid fuelled rocket, typically: that is, the ratio of thrust to weight typically lies between 1.3 and 1.5 . A small solid fuel rocket, on the other hand typically has a thrust much larger than its weight. The difference in performance is marked.

Of course, as the rocket ascends, its mass decreases, and if the thrust is relatively constant, the acceleration of the rocket will increase.

IMPULSE

The concept of impulse relates to the total effect of the thrust over the time that it acts. If the thrust force FT. which may vary over time, acts from a time interval Δt = t2 - t1, then the total impulse on the rocket over the time from t1 to t2 is given by:

If the thrust force remains relatively constant over the time it is acting then the impulse becomes: and substituting FT = ve dm/dt in this situation (where ve and dm/dt are reasonably constant), we find that: which shows that the impulse is the product of the exhaust velocity and the total fuel consumed. The units of impulse are kg m s-1.

There is another type of impulse that is often used in comparing rocket performance, and that is termed the specific impulse Isp. This is defined as the thrust per unit rate of mass loss:

This quantity, unlike other specific quantities (such as the specific density of a fluid) which are dimensionless, has the units of velocity (m s-1). And we can see why when we realise that FT = ve dm/dt (T1). This gives Isp = ve. This of course means that we are simply quoting the exhaust velocity when we mention the specific impulse. And to make matters worse, many engineers define the specific impulse as the ratio of the thrust force to the rate of fuel weight loss (or consumption). This gives a formula for engineering specific impulse as: where go = 9.8 m s-1 is always taken as the gravitational acceleration at the surface of the Earth - even if we are talking about rocket performance on Mars! It has the units of time (seconds), which doesn't relate to the time of burn or any other useful time. So, as you can see, specific impulse is really not a very useful quantity, even though many engineers use it. One might just as well quote the exhaust velocity. Total impulse, on the other hand, is a useful parameter.

However, because you will find specific impulse (the engineering kind) mentioned in many books and journals it is good to note that by simply multiplying this quantity by 10 you have the exhaust velocity of the rocket to within 2% - adequate for most purposes.

FLUID DYNAMICS

To investigate rocket science further we need to investigate the quantities in the rocket equation. In this section we will start to look at the quantity ve, the gas exhaust velocity. The basic physics involved concerns the equations of fluid dynamics. The two of these that are relevant to us are the continuity equation and Bernoulli's equation. Both of these are essentially conservation laws. The first expresses the conservation of mass and the second the conservation of energy.

The Continuity Equation

This equation relates to an incompressible fluid (one whose density is constant) and is concerned with mass flow past a point.

Imagine we have fluid flowing along a tube whose diameter changes. If we have a mass passing one point in the tube each second, then that same mass must pass through any point along the tube in the same amount of time. This can only happen by a change in the velocity of the fluid.

Thus:

Now the mass m passing any point is the cross-sectional area A of the tube at that point times the velocity v of the fluid: The equation of continuity of mass flow where ρ is a constant is thus: Liquid fluids are usually incompressible, whereas gases are compressible. In the case of a compressible fluid, the continuity equation becomes A ρ v = constant. However, in many cases we can still use the equation F1 as long as the density is reasonably constant.

Bernoulli's Equation

Bernoulli's equation expresses the conservation of energy along a streamline of incompressible fluid in non-turbulent flow:

where Po is what the pressure of the fluid would be at a height h in a gravitational field g, and if the fluid was at rest (v = 0). Po is thus a datum pressure of the system at a reference point in the gravitational field which we take as out height datum (h=0).

All the terms in F2 have the units of pressure, which can also be interpreted as energy per unit volume (hence F2 is an expression of energy conservation). The terms Po + ρ g h represent the static pressure of the fluid and ρ v2 / 2 represents the dynamic pressure of the fluid. Another way to express this is that ρ g h is the potential energy density of the fluid while ρ v2 / 2 is the kinetic energy density.

In the absence of a gravitational field, or in zero gravity conditions there is no potential energy contribution (g = 0), and so F2 becomes:

Application to Rocket Propulsion

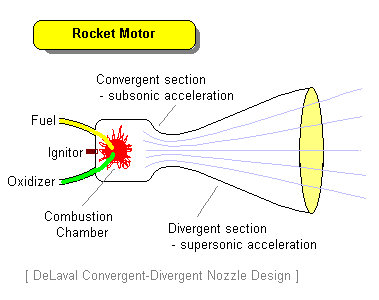
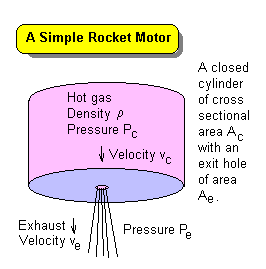Simple rocket motor A very simple rocket motor might consist of a cylinder of high pressure gas with a small exit hole in one end of the cylinder as shown in the adjacent diagram. The cross-sectional area of the cylinder is Ac, whereas that of the exit hole is Ae. The density of the gas inside the cylinder is ρ and the pressure is Pc. The velocity at which the gas inside moves toward the exit is vc.

We now consider a point just outside the exit hole. We can assume that the gas has not yet had time to expand so that the density is still the same as inside the cylinder. However, the velocity and pressure have the values ve and Pe respectively.

Bernoulli's equation in this instance becomes:

which can be solved to give: We can even use this equation in a gravitational field (ie in a planetary atmosphere) because we consider a point just inside the exit and just outside the exit making the difference in the height h term negligible with respect to the other quantities.

By applying the continuity equation F1:

and noting that if Ae is a lot less than Ac then ve has to consequently be a lot greater than vc, which means that the last term in the equation for ve above can be ignored, giving: We have shown above that the thrust on the rocket is: and realising that the rate of mass loss is given by: we can thus show that the formula for thrust in this instance is given by: This would seem to indicate that we need a high internal pressure and a low external pressure to maximise the thrust. The thrust will thus be greater in an external vacuum (outer space) than in an atmosphere, although the difference may not be that great if the internal pressure is a lot greater than the atmospheric pressure.

However, the above equation would also seem to indicate that the thrust will increase as we increase the size of the exit aperture (ie more mass comes out per second). However, we cannot make the exit hole too large or the conditions under which we derived the equation are then no longer valid. Specifically, the internal gas velocity will not be much less than the external velocity and the large internal pressure will quickly dissipate.

THERMODYNAMICS

Only toy rockets use compressed gas as a propellant. Most rockets use a chemical reaction to generate gases as hot as possible. These are expanded through a special nozzle to ensure optimum operation.

Rocket Motor

The laws of thermodynamics which relate to the movement of matter and thermal energy can be used to produce an expression for the exhaust velocity:

where γ is the ratio of the specific heats of the exhaust gas, R is the universal gas constant, μ is the molecular weight of the gas and T = Tc = Te because the process happens so quickly that it is isothermal (chamber temperature and exhaust gas temperature are identical).

In a vacuum, the term in the square brackets [ ] is zero and γ and R are constant giving the approximation:

and k ~ 0.25 when T is in Kelvin to give ve in kilometres per second. This will be modified by the rocket engine design.

It can be seen from the above approximation that a high temperature and a low molecular weight are desirable to produce the largest exhaust velocity. The best conventional fuels are hydrogen and oxygen which combust to produce water vapour with a molecular weight of 18. In an ion engine where protons are accelerated in the engine, the molecular weight is one. However, these engines can so far not throw anywhere like enough mass out the back to give a useful thrust for planetary escape, and so are confined to low gravity conditions. Conventional rocket engines work at temperatures below 3000 Kelvin, and then only because of complicated cooling arrangements which prevent the combustion chamber and nozzle walls from vapourising.

ROCKETRY ON A PLANET

Two main differences exist between rocket operation in space versus rocket operation on a planet. One is due to the presence of an atmosphere, and the second is due to the presence of a gravitational field.

An atmosphere has two effects on rocket operation. Atmospheric pressure works to decrease the effective exhaust velocity of the rocket. The external pressure Pe in the above equations is effectively zero in space and atmospheric pressure on a planet. The degradation in thrust can thus be calculated when the atmospheric pressure is known.

The second effect of an atmosphere is to produce a drag force on the rocket. This drag force opposes (is in the opposite direction) to the thrust force and increases as the rocket velocity increases. The form of the drag force is given by the expression:

where To minimise this drag the velocity can be keep low until most of the atmosphere is cleared. Streamlining will reduce the effective area and/or drag coefficient.

It is difficult to incorporate the drag force into analytical rocket equations because of the dependence on velocity and altitude (through atmospheric density). When it is necessary to compute drag effects it is generally done numerically on a computer where the exact trajectory can be calculated in an iterative process.

Gravity always acts in a vertical direction downwards. If we consider flight only in the vertical direction then by the definition of acceleration (ie time rate of change of velocity) we can write for the case of constant acceleration 'a' over a time interval t:

where and by denoting Δv = v - u as the change in velocity and writing the acceleration as a constant α times the gravitational acceleration g we can write: or As previously stated, for large rockets 1.3 < α < 1.5 at lift-off.

Using equation K1 we can see that gravity reduces the velocity of a rocket by an amount g t in the vertical direction. Including this term in the rocket equation gives us the modified form of the rocket equation in a gravitational field:

which becomes or alternatively Note that equations G1 and G2 are only valid for a constant acceleration (ie when α is constant). Gravity can be assumed approximately constant even to low Earth orbit and the rocket thrust is proportional to the rate of fuel burn which is usually roughly constant in a single rocket. However, as the mass of the rocket decreases, the acceleration (which is inversely proportional to the mass) will increase. If this increase is significant, G1 can be used over a time interval where α is sensibly constant to give a partial 'delta-vee'. G1 can then be applied with a new value of α and so on until the fuel is consumed. All the delta-vee's can then be summed (or integrated) to give the total delta-vee.

MULTISTAGING

The final velocity of a rocket vertically launched from the surface of a planet, at the moment of engine cut-off is given by the equation:

where For a large rocket which initially accelerates slowly and spends only a small fraction of its total flight time in the lower atmosphere, the total drag velocity is usually less than 1% of the total velocity and may be neglected. (This is not the case for small rockets with solid fuel motors that achieve a high acceleration very quickly).

If we use equation G2 and assume a constant acceleration, we can plot a graph showing the mass ratio required at different exhaust velocities to achieve a specified velocity.

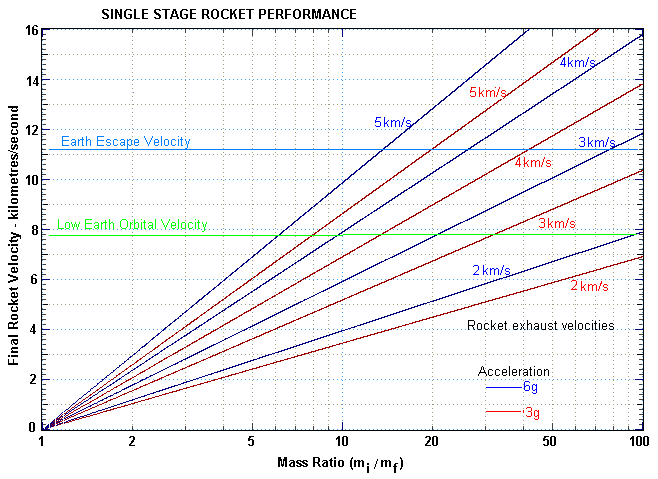
Rocket performance

Now a maximum practical mass ratio for a large rocket is about 10. This means that the final mass is 10% of the initial mass, which allocates 90% of the mass to the useable fuel and 10% of the mass to the rocket structure itself plus tanks, engines, control systems and payloads. For an acceleration of 3g (α=3) it requires an exhaust velocity of 4500 m/s to achieve a mass ratio of 10, if the rocket is to achieve orbital velocity. This exhaust velocity is higher than the best chemical propellants (hydrogen - oxygen) can achieve. This is why a single stage to orbit rocket has not yet been developed.

To achieve orbital velocity and higher we must (so far) use multistage rockets.

Consider a 3-stage rocket with an acceleration of 3g and an exhaust velocity of 3500 m/s. If the mass ratio for the first stage is 3 (ie fuel is 67% of the first stage mass plus the mass of the two subsequent stages) then the first stage will achieve a velocity at burnout of 3 km/s. At burnout the first stage drops away leaving the remaining two stages. If the following two stages have a similar mass ratio (after losing the stage mass below them) they will each add a delta-vee of 3 km/s for a total velocity of 9 km/s which is adequate to achieve low Earth orbit. We can write the total velocity achieved vT as the sum of the delta-vee's of each stage:

where there are n stages, and where ts is the total interstage timing loss (ie the time between stages when no engine is operating).

In the above example we have assumed that the parameters of each stage are identical. This is unlikely to be the case and in practice each stage will have a different mass ratio, a different acceleration and possibly a different exhaust velocity.

REFERENCES



ASAAustralian Space Academy