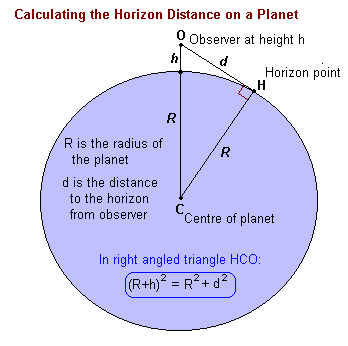
An observer looking out on a spherical world can only see a limited distance - to a line we call the horizon. The distance to that horizon depends only on the height of the observer and the radius of the planet.

Applying the theorem of Pythagorus to the triangle we have
The above formula is useful when standing on land looking out to sea. However, in practice the surface of a planet is usually quite irregular and we then need to apply this formula twice to compute the distance to the topographic horizon.
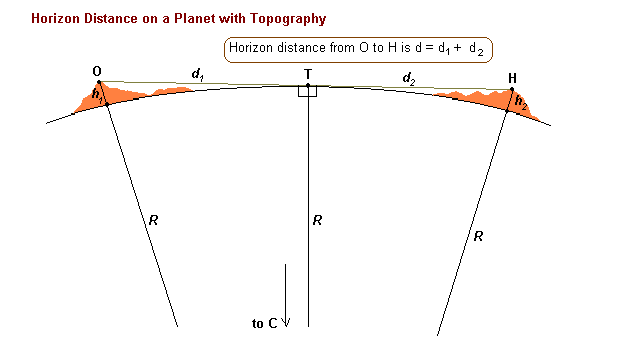
In this case the horizon distance h is given by:
Note that in all the above equations, it is essential that the same units are used for the planetary radius and the observer height. This will then give the horizon distance in the same units. Anythng else requires a conversion factor.
The following table compares horizon distances for 'flat' parts of the Earth (RE = 6371 km), the Moon (RL = 1737 km) and Mars (RM = 3390 km). Note that these radii are mean radii. The observer heights are in metres, but the horizon distances in the main part of the table are in kilometres.
| HEIGHT | EARTH | MOON | MARS |
|---|---|---|---|
| 1 m | 3.57 | 1.86 | 2.60 |
| 2 m | 5.05 | 2.64 | 3.68 |
| 5 m | 7.98 | 4.17 | 5.82 |
| 10 m | 11.3 | 5.89 | 8.23 |
| 20 m | 16.0 | 8.34 | 11.6 |
| 50 m | 25.2 | 13.2 | 18.4 |
| 100 m | 35.7 | 18.6 | 26.0 |
To extend the table note that the entries for h=100 are simply ten times the entries for h=1. Thus the entries for h=200 will be ten times the entries for h=2 and so on.
For other non-tabulated values of h, use the formulae:
 Australian Space Academy
Australian Space Academy