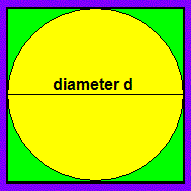
-
Circle diameter = d
Circle circumference = pd
Circle Area = pd2/4
Square Area = d2
Ratio of areas = p/4
In scientific studies we often come across constants of nature that relate one part of the universe to another. Probably the best known of these is the ratio of the diameter of a circle to its circumference. This constant is designated by the greek letter pi ( p ).
 |
Circle circumference = pd Circle Area = pd2/4 Square Area = d2 Ratio of areas = p/4 |
This constant pops up in many different places, probably the most profound is the inverse square law. This expresses the fact that as radiation (such as light or radio waves) spreads out in space, its intensity diminishes as the square of the distance from the source. This is an intrinsic property of three dimensional cartesian space.
SPACE ENVIRONMENT FORMULAE
In the field of space weather there are many formula in which p appears.
When ionospheric electrons move around in the F-layer, they are moving through the Earth's magnetic field. This causes them to spiral around the field lines as they move forward, tracing out a helical path. The frequency of the periodic motion is called the cyclotron frequency and is given by the formula:
where
This frequency also applies to the motion of any charged particle in a magnetic field (eg electrons in the magnetic fields around sunspots).
Another important frequency is given by the formula:
This is called the plasma frequency. Ne is the electron density in the plasma, and e is the plasma permittivity. Any plasma (such as the solar corona or the Earth's ionosphere) exhibits this natural resonant frequency according to the number of electrons present in each cubic metre of the plasma (ie the plasma density). It is the frequency at which the electrons will oscillate about the ions if the plasma is disturbed. It is also most importantly the frequency below which the plasma becomes opaque (radio waves cannot penetrate but are reflected from and by the plasma), and above which it appears transparent to radio waves, although like glass to light rays, it will refract such waves passing through it.
The p in the above formulae appear because of the geometry of space. To someone standing at the centre of a circle, its circumference subtends an angle of 2p radians. Other formulae may contain p because in three dimensions, a sphere subtends an angle of 4p steradians at the centre.
CALCULATING PI
The value of the constant pi has been of interest to mankind throughout the ages. At the time of Archimedes (around 250 BC), it was known to at least 3 decimal places. However, pi is a transcendental number, and has an infinite number of decimals. Only through exhaustive calculation can we find even a small portion of this infinite series. With modern computers pi has now been calculated to over 50 billion places.
Many calculation methods rely on a series expansion for the arctangent relation to compute pi. This is given by:
This series converges only when X is less than or equal to one. When x=1 we have that arctan(1) = p/4. Thus the first series we might try would be:
Although this formula will work, it converges to the correct value of pi very slowly, requiring about 7000 steps just to find the first 3 decimal places of pi. A much more useful formula is given by the relation:
PI TO 1000 DECIMAL PLACES
The value of pi to 1000 decimal places is listed below:
3.1415926535 8979323846 2643383279 5028841971 6939937510
5820974944 5923078164 0628620899 8628034825 3421170679
8214808651 3282306647 0938446095 5058223172 5359408128
4811174502 8410270193 8521105559 6446229489 5493038196
4428810975 6659334461 2847564823 3786783165 2712019091
4564856692 3460348610 4543266482 1339360726 0249141273
7245870066 0631558817 4881520920 9628292540 9171536436
7892590360 0113305305 4882046652 1384146951 9415116094
3305727036 5759591953 0921861173 8193261179 3105118548
0744623799 6274956735 1885752724 8912279381 8301194912
9833673362 4406566430 8602139494 6395224737 1907021798
6094370277 0539217176 2931767523 8467481846 7669405132
0005681271 4526356082 7785771342 7577896091 7363717872
1468440901 2249534301 4654958537 1050792279 6892589235
4201995611 2129021960 8640344181 5981362977 4771309960
5187072113 4999999837 2978049951 0597317328 1609631859
5024459455 3469083026 4252230825 3344685035 2619311881
7101000313 7838752886 5875332083 8142061717 7669147303
5982534904 2875546873 1159562863 8823537875 9375195778
1857780532 1712268066 1300192787 6611195909 2164201989
Programs to calculate pi, and methods to memorise at least the first 35 digits of pi can be found on various web sites.
HOW RANDOM IS PI?
The digits of pi appear to obey the statistics of random numbers. That is, in one hundred digits of pi we would expect to find approximately 10 zeroes, 10 ones, 10 twos, etc. Not exactly ten for each number, as statistical fluctuations occur. In fact, for the first 100 digits of pi, the values are:
Digit Occurrence
0 8
1 8
2 12
3 11
4 10
5 8
6 9
7 8
8 12
9 14
Counting only 100 digits we see quite a variation in digit occurrence or frequency. Nine is clearly more prominent in the first 100 digits of pi than is any other digit. However, as we consider more and more digits the average frequency of each should approach 10%. This does not rule out long sequences of a single number, say twelve fours. In fact, in a infinite string we might expect to find any combination of numbers that we could think of. We would just need to be infinitely patient to find them.
Thus in any finite search of the digits of pi we would be rather suspicious if we found a series of only ones and zeroes that went on for say 169 digits. And what if these digits went like this:
000000000000000001111100000001001001000001000 100010001000010000100100001000010011111111111 001000010000100100001000010001000100010000010 010010000000111110000000000000000
Carl Sagan postulated a similar scenario in his novel CONTACT.
Read the book, and particularly the last chapter for what
this might mean!
|
"For since the creation of the world, God's invisible
qualities - his eternal power and divine nature - have
been clearly seen, being understood from what has
been made, so that men are without excuse." |
| Romans 1:20 |