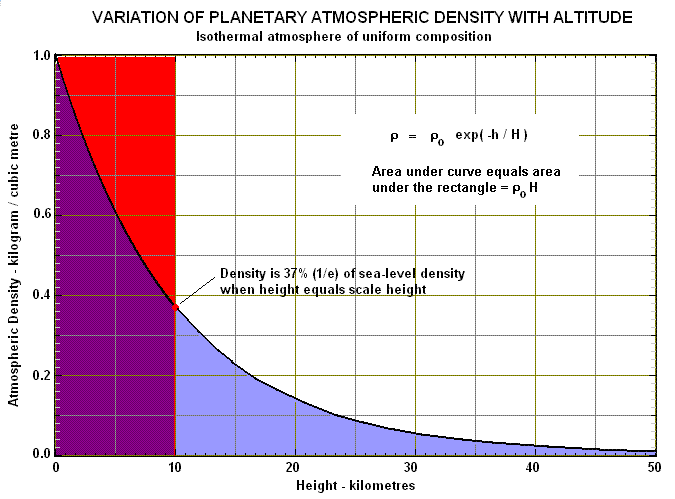
A body such as a planet or star that has an isothermal atmosphere of uniform composition shows a variation of density (ρ) with altitude (h) that can be written as:
where ρ0 is the density at a reference level (such as sea-level for a planet like the Earth), and H is a constant called the scale height of the atmosphere. This relation is shown in graphical form below:
The scale height is related to the temperature (T) and mean molecular mass (m) of the atmosphere by the formula H = kT/mg where k is Boltzmann's constant and g is the gravitational acceleration of the body. The scale height is a very useful concept because it is the height at which the atmosphere would extend if it were all compressed into one of constant density (the rectangular area in the above diagram). At this height the real atmosphere has a density of 1/e or 0.37 of its density at the reference level. The scale height is also a measure of the atmospheric density gradient - a lower scale height implies a higher gradient.
Although no real atmosphere is truly isothermal and of uniform composition, the above approximation can be used over limited height ranges (eg. on Earth, H ~ 10 km over the range from 0 to 100 km). Different altitude ranges are then characterised by different scale heights.
Australian Space Academy