NOISE TEMPERATURE, NOISE FACTOR and NOISE FIGURE

INTRODUCTION

Noise is ubiquitous in all communication systems. This noise may originate in the receiving system itself, and it is also present throughout the universe. It has a Gaussian or Normal distribution (bell-shaped curve), and can be characterised by a quantity we call the noise temperature T_n, which has the units of absolute temperature (Kelvin).

There is a power associated with the noise temperature, and this is the power delivered by a passive matched load (eg a resistor) that is attached to the input of a receiver. This power is given by the formula:

P_n = k T_n (W Hz^-1)

P_n = k T_n B (W)

If the receiver is not connected to an antenna then the noise measured at the receiver output is only due to the noise generated in the receiver itself. This noise is usually referred to the receiver input and this input power is associated with a noise temperature that is called the receiver system temperature T_sys. This temperature is what sets the limiting sensitivity of the receiver. The lower this temperature the better the receiver.

A poor receiver may have a system noise temperature of several thousands of degrees Kelvin. A medium quality receiver may have a system temperature of several hundred Kelvin, and a good receiver a noise temperature below 100 K.

Note that if a communications receiver is pointed to a region of the sky near the galactic centre where the sky noise may be several thousand Kelvin, then there is no point is striving to have a receiver noise temperature below 100 K, because in this case the system noise temperature will be determined by the background sky noise, not the receiver noise.

ENGINEERING NOISE UNITS

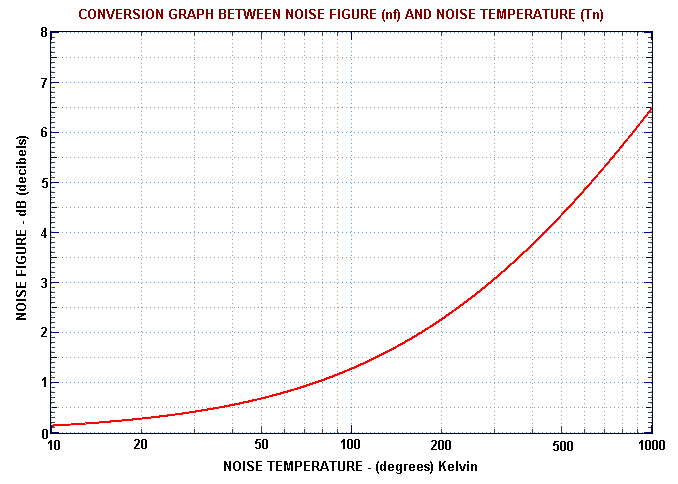
Receiving systems that require a very low noise temperature often employ a low noise amplifier (LNA) that is placed very close to the antenna (to avoid cable losses). These amplifiers are characterised by two quantities: their noise performance and their overall gain. Often the internal noise is specified by a noise factor F or a noise figure nf. These are units used by engineers. However, there are simple formulae that relate F, nf and T_n.

The engineering quantity noise factor F is defined by assuming that the antenna is looking at an object which has a temperature equal to 'room' temperature, which is 'defined' as T₀ = 290 K. The actual noise power measured (referred to the receiver input) is then due to both the external noise source at 290 K and the internally generated receiver noise T_n. The system noise temperature in this case is T_sys = T₀ + T_n.

Engineers write that T_sys is a multiplicative factor F of the arbitrary temperature T₀. That is:

T_sys = F T₀

T_sys = T_n + T₀

T_n = (F - 1) T₀

nf = 10 log₁₀ F       (dB)

SKY NOISE TEMPERATURE

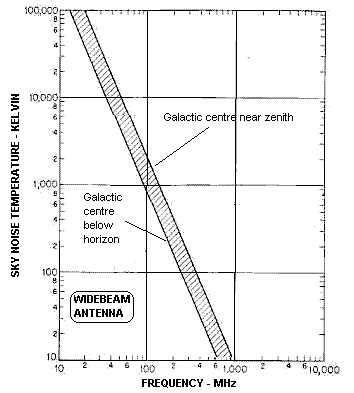
Astronomical radio sources in the sky are a source of noise for receivers with antennae pointing skyward. It is often useful to know the value of the effective sky temperature and how it varies with frequency. The graph below left shows the effective sky temperature for a wide beamwidth antenna.

By far the greatest noise generator in the sky lies at the center of the milky way, and if this lies in the beam of the antenna the noise temperature will be greater than when the galactic center and most of the galactic plane lies below the horizon. The two lines at the extremes of the hatched region indicate the minimum and maximum noise temperatures to be expected for these two extreme conditions. The actual noise temperature experienced will thus lie in the hatched region between these two conditions.

Low Noise Amplifiers

Australian Space Academy