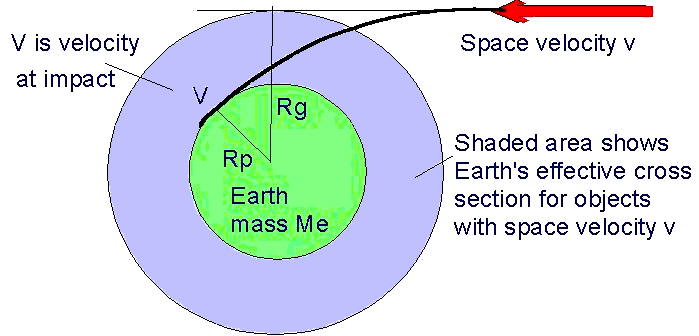
For a projectile to hit a target it normally must impact within an area which is the cross-sectional area of the target. For a spherical body, this area is π r2 where r is the radius of the sphere. However, in the case of a meteoroid or an asteroid impacting the Earth (or another planet), the appropriate cross-sectional radius is not the physical radius of the Earth, but its gravitational radius, which depends upon the impactor velocity.

This is because the Earth's gravity will attract an impactor that might be approaching on a near miss orbit. Imagine we have an impactor that in the absence of gravity has a space velocity v, and is on a trajectory with a distance Rg from the Earth's centre. Because of gravity the trajectory will curve toward the Earth and impact with a velocity V.
This impact will be tangential if Rg is the gravitational radius of the Earth for the space velocity v (ie the body just impacts the planet). We can use the laws of conservation of momentum and conservation of energy to determine Rg.
|
v Rg = V Rp (conservation of momentum) |
where G is the universal gravitational constant. Solving these two equations simultaneously we find that:
|
Rg = Rp * SQR[ 2 G Me / ( v2 Rp ) + 1 ] |
The table below presents values of Rg (as a function of the space velocity), both in kilometres and as a fraction of the Earth's radius. Also shown are the fractional area (the effective cross-sectional area seen by the meteoroid, relative to the Earth's cross-sectional area) , and the collision velocity.
Space |
Collision |
Effective |
Fractional |
Fractional |
|
2 |
11 |
36237 |
5.68 |
32.26 |
We can see from this table that bodies with an initially low velocity are affected the most. Their change in velocity is greater, and they will be captured at a greater radius than will the higher velocity objects.
 Australian Space Academy
Australian Space Academy