Asteroid-Satellite Collision Probability

ASTEROID-SATELLITE COLLISION PROBABILITY

INTRODUCTION

On the 23rd of February 2012 at the OAM Observatory in La Sagra, Spain a new asteroid was discovered. It was only a small asteroid, estimated to have a diameter of about 45 metres and a mass of 130,000 tons, but what made it interesting was its orbit. Calculations showed that it would pass very close to the Earth. Not close enough to hit, but so close that it would pass by at a distance closer to the Earth than that of geosynchronous satellites.

The asteroid currently goes by the designation 2012 DA14, and its closest approach to Earth will occur on 15 Feb 2013 at 19:25 UT, with a best estimate radial miss distance of 35,000 km (this is a distance of about 29,000 km from the Earth's surface). Goesynchronous satellite orbital radius is 42,000 km.

The natural question to ask is whether it might hit a satellite? Australia has several communication satellites in geosynchronous orbit. These provide many services to civilian and military users throughout Australia and overseas. Apart from television programs, vital aviation communications are relayed by geocomsats. Sudden loss of such a satellite would cause significant problems, some involving human safety.

This note will show how approximate collision probabilities may be calculated.

Is a collision between an asteroid and a satellite likely?

DYNAMICS

Strictly geostationary satellites are located above the Earth's equator fixed at a specific longitude. In practice few satellites are truly geostationary, but they are still geosychronous. To minimise station keeping they are allowed to wander a little around their assigned latitude and longitude. As seen from the Earth they move in a small figure of eight centred on their nominal position. This is mostly because their orbital inclination is not exactly zero. At the start of life a controlled geosat will probably be maintained with an inclination of less than one degree. However, some satellites, particularly non-commercial geosats, may be given or allowed to have inclinations of up to 30 degrees, especially a valuable satellite whose station keeping fuel is mostly expended.

The diagram below is a snapshot in time of all large space objects in high Earth orbit. Drawn in 2009, this shows all objects larger than about 30 cm, a mixture of active satellites and space debris. The geostationary ring can be clearly seen, with satellites closely confined to the equatorial plane. Other objects are below geosynchronous orbit, high inclination geosats, geosynchronous transfer orbits, or in supersynchronous orbit (where most geosats are placed at the end of their life.

Snapshot of Space Objects in High Earth Orbit - 2009 (NASA/ODPO)

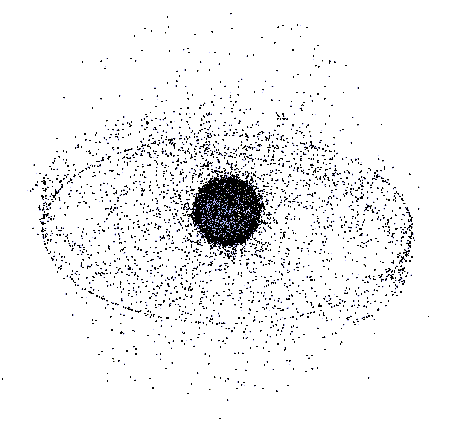
As can be readily seen from this diagram, an asteroid can easily pass closer to the Earth than geosynchronous altitude without going anywhere near the ring of nearly geostationary active satellites. In fact it is more likely to do so than to spend any time in the geostationary ring.

If we know the orbital details of the asteroid, we can compute its trajectory past the Earth, and thus know whether it will pass near the geostationary ring (ie within a few hundred kilometres, which is the normal station keeping distance of an active geosat).

In the case of asteroid 2012DA14, it will not come near any geostationary satellites, as can be seen in the trajectory diagram below.

NASA/JPL/NEO diagram of asteroid 2012DA14 passing near Earth

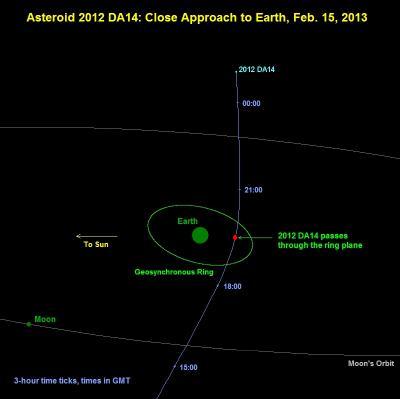
The asteroid does pass through the equatorial plane, which is the same plane as geostationary orbit, but it is not at geosat altitude when it does so. Thus, in this case the risk to true geostationary satellites is zero. However, it is possible that the asteroid could pass close to satellites that have high inclination geosychronous orbits.

In the case where we know only the miss distance of the asteroid but not its full orbital dynamics (although this is unlikely) we can calculate the probability that it might hit a satellite. We actually emplopy a simplified model in which we assume that all the active satellites (ie the ones in which we are interested) are not in a ring or torus around the Earth, but are spread out uniformly in a spherical shell surrounding the Earth at geosat altitude. This is equivalent to not knowing the path of the asteroid as we shall show later on.

A SIMPLIFIED MODEL

The diagram below is a cross-section drawn in the plane of the asteroid's motion. We make a number of simplifying assumptions. First we consider that the asteroid moves in a straight line. In actual fact its motion will be curved because of the Earth's gravitational pull (the curvature due to its orbit around the Sun can be neglected over the relatively short distances considered here). The effect of the neglected curvature will be to slightly increase the probability of collision. We can compensate for this by decreasing the minimum miss distance. However, this approximation, like the others involved in this calculation, are negligible if we only require an order of magnitude calculation (ie within a power of ten).

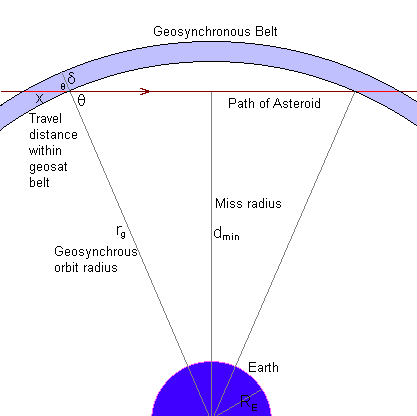
The thickness of the spherical shell in which we assume the satellites reside is δ. It is only a few hundred kilometres in thickness, and as long as it is a lot smaller than the geosat radius (r_g) the exact value does not even matter, as it disappears in our equations. Note that d_min is the miss radius, not the closest distance to the nearest point on the Earth surface. For our approximate calculations we will take r_g as 36,000 km and R_E as 6000 km.

First we compute the number density of active satellites in the spherical shell we have drawn. The approximate volume of this shell is its surface area (4 π r_g²) times its thickness δ. Thus:

_geo

The number density is then given by:

_geo

The distance that the asteroid travels within the shell is:

_min

The factor of 2 is because the asteroid both enters and exits the shell (left and right red sections in the diagram). The expression for cos θ is given from the value for sin θ in the large triangle, and use of the identity cos²θ + sin²θ = 1.

We now assume that the asteroid has a size (this could be an average diameter) of α and thus a cross-sectional area to its direction of travel of approximately α². The volume of space that the asteroid traverses in the spherical shell is then given by:

_min

The number of satellites in this volume (ie in the path of the asteroid) is:

_hits

_geo

_min

This is the final equation we need for our calculation. Note that the quantity δ does not appear here.

We will assume there are around 1000 satellites in geosynchronous orbit. The size of 2012DA14 is 45 metres. If you are concerned that we ignored the size of the geosats you can increase this size to 50 m (assuming an average geosat sixe of 5 m), but it doesn't make much difference in the final result. If we assume that the miss radius of the asteroid is 35,000 km, then we find that

_hits

^-10

This is the average number of satellites we can expect to be hit during close passage of the asteroid past the Earth. To have an average of one satellite hit we need to increase this number to around unity. This would require about 3 x 10⁹ passes by asteroids of similar size. Thus we can say that the probability of collision from a single pass is less than one in a billion.

Astronomers estimate that there are around one million near Earth asteroids with a size of 100 metres or greater. These are asteroids that could pass near the Earth. A rough formula relating numbers of such asteroids (N) to their size (d) in kilometres is:

_nea

This formula gives around 8 million bodies of 50 metre size (equivalent to 2012DA14). Compared to the number of asteroids required to damage one satellite, as given above, this should make us confident that asteroids do not pose any significant threat to satellites in geosynchronous orbit.

DISCUSSION AND JUSTIFICATION

Astute mathematicians may notice that the formula for the distance that the asteroid travels in the spherical shell becomes infinite when the minimum approach distance is just equal to the geosychronous radius. This singularity can be avoided by the inclusion of a third term in the radical, giving:

_min

We now need to justify the use of our shell model. Using different subscripts, we can write the number of hits for our shell model as:

_hits(shell)

_shell

where ρ_shell = N_geo / V_shell

For the case of a ring model, where the geosats all lie in a ring or torus in the equatorial plane (as they do in reality), the formula becomes:

_hits(ring)

_ring

where ρ_ring = N_geo / V_ring and where f_ring is the fractional ratio of the ring volume to the shell volume. This is essentially the probability that the asteroid will pass through the ring volume. That is:

_ring

_shell

Simple substitution shows that

_hits(ring)

_hits(shell)

Our simplified model is thus equivalent to reality. There may be a factor of two difference according to whether the asteroid makes one or two passes through the ring, the former case being the more likely. However, this is still well within our order of magnitude estimate.

THE METEOROID HAZARD

Small bodies are much more numerous than are larger ones. It is easy to show that meteoroids present a much greater hazard, albeit still very small, than do the larger asteroids.

We will assume that meteoroids of around one centimetre in size have enough energy to cause damage to a satellite. In this case the collisional cross-sectional area is set not by the meteoroid but by the size of the satellite (s).

Let us designate the terrestrial meteoroid flux by F (number per unit area per unit time), and use our shell model. The number of meteoroids passing through the shell in unit time is the flux times the area of the shell:

The number of satellites hit by this number of meteoroids ( that travel an average distance of about 2 δ in the shell) in a time t is:

_m-hits

_geo

We can turn this around to compute the average time T it would take to have one satellite hit:

_geo

A typical active geosat might have an average size of s = 5 metres. The meteoroid flux around the Earth for particles one centimetre in size is F = 10^-6 per square metre per year. Assuming 1000 active geosats, we can use the above formula to calculate a value of T = 20 years for one satellite to be hit on average. Thus we can conclude that the small bodies that produce meteors in our sky every night (and day) are considerably more of a hazard than are asteroids.

Meteoroids pose a greater, although small, threat to satellites
Credits: Left image - Desert Fireball Network, Right image - European Space Agency

SUMMARY

The probability that asteroid 2012DA14 will damage an active geostationary satellite is zero.

The probability that an asteroid of similar size (about 50m across) might damage an active geosynchronous satellite in the future is less than one in a billion.

There are estimated to be 8 million near earth asteroids of this size. They thus do not constitute a significant threat.

Meteoroids around one centimetre in size pose a much greater threat, although still very low. These small bodies can be expected to damage one active geosat every 20 years.

January 2013

ASA Australian Space Academy