It is a rule of flying that if another aircraft remains on
the same relative bearing then an impact is likely. That is,
if you look to your right and notice that a red biplane is
at your two o'clock position and remains there for a time,
increasing in apparent size, then a collision will result
unless one or both aircraft take evasive action.
The same rule applies to objects in space, if velocities remain constant. What is significant is that it is possible to predict the time of impact, even though the size and distance to the impactor are both unknown. The cosmologist Fred Hoyle pointed this out in his science fiction novel "The Black Cloud".
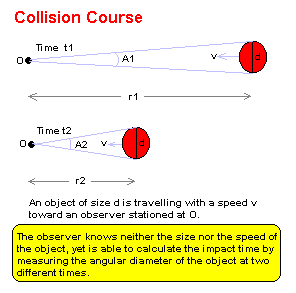
Consider the diagram below:

The unknown object has a size d across, and it is heading toward the observer with a speed v. Both its size and its speed are unknown to the observer, as well as the distance it is away. With all these unknowns, it might appear inconceivable that we can calculate the time of impact. However, with just two measurements, this can be done.
The observer must measure the angular diameter of the object at two times, ideally separated by enough time so that the apparent size increase of the object is significant (such as a doubling of size).
Let the angular size of the potential impactor be A1 at a time t1 and A2 at a time t2. Note that these angular sizes must be expressed in radians where one radian is equal to 57.29578 degrees.
Then the size of the object is given at each time by:
Solving these three equations gives the time to impact as:
There is a special case to consider here. If the object doubles its apparent angular size (ie A2 = 2 A1) in a certain time, then impact will occur in the same time again. For example, if the object doubles its apparent size from February 8 to February 15 ( 7 days), then we can expect impact on February 22 (another 7 days).
We don't need to wait for a doubling of size to apply the above formula. If we can measure the object's size with a high degree of accuracy, we can potentially calculate the impact time with only a 1% increase in size. However, the greater the increase in apparent size, the greater the accuracy of our prediction. It is a case of balancing accuracy against time (in which we may be able to take some evasive action).
All of the above assumes that the relative velocity of the object to the observer remains constant. For bodies that travel appreciable distances under the action of gravitational forces (eg in orbit around the Sun), this will not be so. Thus this simple result cannot be applied to an asteroid collision many months in advance. However, it can be applied over short periods of time, and also where any velocity changes due to gravitational effects are small with respect to the impact velocity. The latter case could apply to an extremely fast interstellar projectile entering the solar system. In general, only an elaborate computer program using highly refined orbital mechanics can really determine whether collision is likely or not.
 Australian Space Academy
Australian Space Academy