

In 1992 Duncan Steel presented a paper at a conference in Adelaide suggesting that it might be useful to consider the detection of a class of near Earth objects through their transit of the solar disc. One such class of objects is the Aten asteroids (with periods less than one year). Another group may be comets that have just completed perihelion transit at a distance less than 1 AU. These objects would be approaching the Earth from the sunward direction, a blind spot to conventional astronomical searches.
One of the reasons for considering NEO detection via solar transit is that there are many stories over the last few centuries which relate objects being observed moving across either the solar or the lunar discs, and which appear hard to explain via local phenomenon occuring in the Earth's atmosphere. (Although to counter this, we have no record or such phenomena occuring at Learmonth Solar Observatory, where the Sun is monitored continuously from sunrise to sunset every day of the year.
A number of short programs in the Microsoft BASICA/GW-BASIC language were written to evaluate the potential of an NEO solar transit system. These are presented here to allow others to experiment with the concept. Note that these programs can also be run under the more readily available QBASIC interpreter. Each program can be "cut" from this page and pasted into a text file NEASOLn.BAS, and then run under the QBASIC interpreter.
HOW BIG?
The first question we asked was how big an object has to be to be detected by a solar telescope? That is, what is the angle subtended by an NEO to an Earth observer?
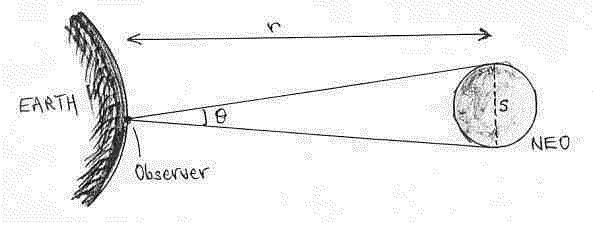
The angle subtended by an object of linear dimension 's' at a distance 'r' is given by:

Program NEA1 was written to tabulate 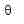 for:
for:
The program listing is given below:
10 '[ NEASOL1.BAS ] - NEO ANGLE SUBTENDED TO OBSERVER 19 ' 20 'setups 21 ' 22 DIM S(7),A(7) 'asteroid size and angle subtended 24 S(1)=10:S(2)=30:S(3)=100:S(4)=300 'set up asteroid sizes 26 S(5)=1000:S(6)=3000:S(7)=10000 'from 10m to 10 km 28 F$="####### ####.# ####.# ####.# ####.# ####.# ####.# ####.#" 29 ' 30 'headings 31 ' 32 LPRINT:LPRINT 'printout is to printer LPT1 on parallel port 34 LPRINT ,,"NEAR EARTH ASTEROIDS" : LPRINT 'print headings 36 LPRINT ," ANGLE (ARC-SECONDS) SUBTENDED TO OBSERVER" 38 LPRINT:LPRINT 40 LPRINT " Range",,"Linear size (metres)" 'headings for table 42 LPRINT " (Km) 10 30 100 300 1000 3000 10000" 44 LPRINT 49 ' 50 'calculations 51 ' 52 FOR R=20000 TO 1000000! STEP 20000 'R is range in km 54 RM=R*1000 'range in metres 56 FOR I=1 TO 7 'step through asteroid sizes 58 A(I)=206000!*S(I)/RM 'angle in arc-seconds 60 NEXT I 62 LPRINT USING F$;R,A(1),A(2),A(3),A(4),A(5),A(6),A(7) 'print table 64 NEXT R 69 END
The output of the above program is shown here:
The shaded section represents the typical resolution limit that will be experienced by an average Earth-based small aperture solar telescope (about 2 to 3 arc-seconds, generally limited by seeing conditions). That is, only objects within the shaded area will be visible. This means that for a 1 km NEO to be observable it must come within 100,000 km of the Earth (a little under a third of the distance to the Moon).
The program may be readily changed to accomodate a different range of variables. Object sizes may be changed through reassignment of the values to the "S" array in lines 24 and 26. The range span may be readily changed by adjusting the start, the final and the step values in the FOR loop in line 52.
OBSERVATIONAL LIMITSA digression about telescope resolution, seeing and telescope aperture.
It is turbulence in the troposphere (lower 10 km of the atmosphere) that produces refractive "cells" with dimensions from around 75 to 250 mm. The lifetime of these cells is only about 0.05 seconds, and they may move with winds aloft up to 200 km/hour. These cells deviate the light passing through them and at night limit resolution to around 0.7 seconds of arc, and daytime resolution to about 2 seconds of arc.
The theoretical resolution of a telescope with an objective aperture "a" is given approximately by the Rayleigh criterion:

For white light with an average wavelength of 500 nm, we can determine that the minimun objective size to achieve 2 arc second resolution is

For this to project a white light image such that a 2 arcsecond object will be detectable, we need to consider that the resolution of the eye is around 100 arcsecond for light conditions (decreases to 20 arcsecond in dark conditions). With an average viewing distance of 50 cm, this implies a solar disc size of around 20 cm. An objective of only 50 mm probably does not collect enough light to useful image this size. A 100 mm telescope is probably the smallest size that can achieve the atmospheric limited resolution of 2 arcseconds.
HOW FAST?
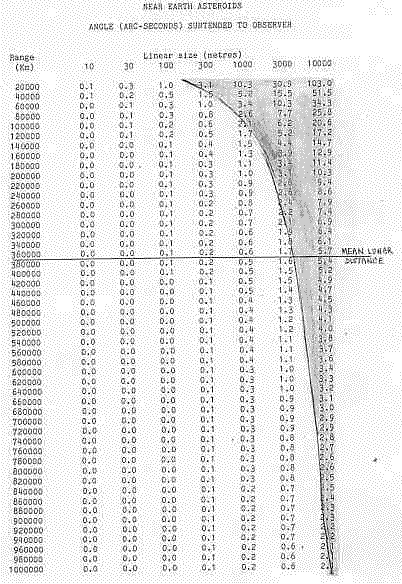
The next question we need to ask is how fast will an NEO appear to move across the solar disc? Or, what is the apparent angular motion of an NEO to a solar observer.
A body in an orbit very similar to the Earth will show very little motion to a geocentric observer. However, an observer on the Earth's surface will see an apparent motion due to the Earth's rotation. This will in provide an indication of what lover bound might be expected to an NEO observed angular speed.
With reference to the above diagram we have that r
Differentiating this with respect to time we have:
The Earth's radius is around 6000 km and if we take an NEO distance
of 50,000 km (if this is too great our initial assumptions may
become invalid), and knowing that the Earth rotates 360 degrees in
24 hours, we have that:
( The analysis will be different if considered at sunrise or sunset
rather than at central meridian passage, and we have ignored the very
small angular motion of the Sun (one degree per day due to the Earth's
orbital motion). However, the figure here gives us an order of
magnitude estimate. )
The fastest angular motion that we might observe will be from a body
travelling in a highly elliptical orbit with a perigee at 1 AU and
travelling with retrograde orbital motion (inclination = 180 degrees).
This would be highly unusual, but it does give us an upper bound
with which to work.
The maximum actual velocity can be approximated by solar escape
velocity at Earth orbit:
To this we must add the Earth's orbital velocity of 30,000 m/s.
This gives us a maximum speed of 72,000 m/s (note: the Leonid
meteoroids are actually observed with velocities very close to
this - so we know it does occur!)
Substituting v = 72,000 m/s for a very close approach (say r=20,000 km)
we have :
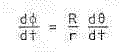
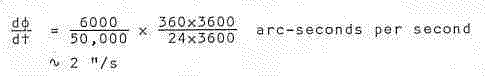
FASTEST MOTION

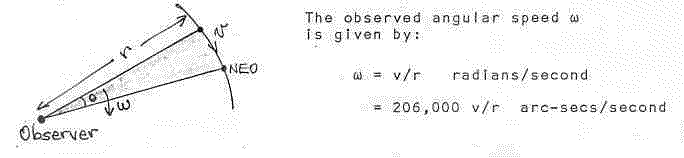
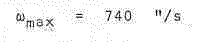
We can thus summarise our discussion by stating that the expected range of observed angular speeds for observable NEOs transiting the solar disc is from about 1 to 1000 arcseconds per second.
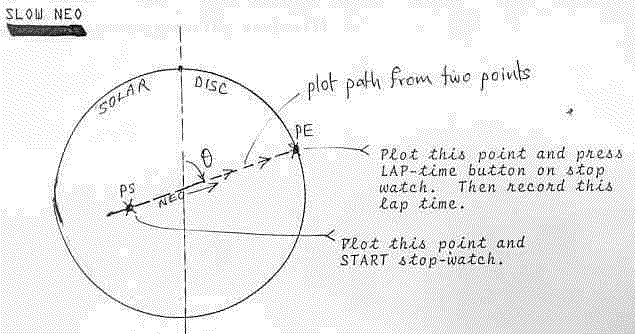
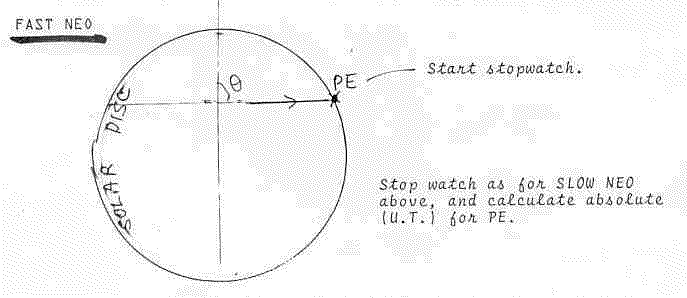
SIMULATION OF NEO SOLAR TRANSITS
Program NEA2 was written to simulate the passage of small NEOs across the solar disc.
The program simulates a dark body with angular dimensions of 5 by 10 arcseconds moving at expecte angular velocities across the bright solar disc of diameter about 2000 arseconds (the actual mean value is 1919 arcseconds).
The simulated NEos have velocities, chosen at random, from 30 to 1000 arcseconds per second of time, giving transit times across the full solar disc of from 2 to 60 seconds. Their transit across the disc is made by a random choice of the entry and exit angles. They may thus appear to cross anywhere (in a chord) across the disc.
The program is written in GW-BASIC and will run under this interpreter or a QBASIC interpreter on a PC/XT/AT/386/486/Pentium or compatible computer. It uses CGA graphics mode, but this is available on practically any video card likely to be encountered on a PC (eg SVGA). The screen resolution in this mode is 640 x 200 pixels.
The program source code is presented below:
100 'NEASOL2 - Simulates near Earth asteroids crossing solar disc 101 ' 199 ' 200 'setups 201 ' 220 SCREEN 2: KEY OFF: CLS 222 AR = .417 'screen aspect ratio 224 PI = 3.14159 'circle circumference/diameter 226 RANDOMIZE (TIMER) 'remove this line for repeatable transits 228 N = 0 'counter for number of NEA transits 299 ' 300 'draw sun on the screen 301 ' 320 CIRCLE (320, 100), 200, , , , AR 'one x-pixel = 5 arc-seconds 340 PAINT (320, 100) 'fill in circle (white) 399 ' 400 'get entry and exit point 401 ' 410 SPA = RND * 2 * PI 'entry/start position angle 412 FPA = RND * 2 * PI 'exit/finish position angle 420 SX = 200 * COS(SPA) 'now put in rectangular coords 422 SY = 200 * SIN(SPA) 'don't yet centre on screen 424 FX = 200 * COS(FPA): FXS = FX + 320 'or correct for aspect ratio 426 FY = 200 * SIN(FPA) 'fxs is for transit end test 499 ' 500 'compute velocities and plot first point 501 ' 510 V = 30 + RND * 970 'speed in arc-seconds per sec 512 'velocity is randomized to give a total transit time across the full 514 'solar diameter (about 1919") of from 2 to 60 seconds 516 V = V / 5 'corrected to screen pixels 520 R = SQR((FX - SX) ^ 2 + (FY - SY) ^ 2) 'traversal distance - arc secs 530 XV = (FX - SX) * V / R 'x speed arc secs per second 535 YV = (FY - SY) * V / R 'y speed arc secs per second 560 OPX = SX + 320 'compute first 565 OPY = SY * AR + 100 'screen coords 570 T0 = TIMER 'simulation start time now 580 PSET (OPX, OPY), 0 'start NEA at limb of sun 599 ' 600 'perform transit motion 601 ' 610 T = TIMER: DT = T - T0 'get new time 612 NPX = SX + XV * DT + 320 'new screen x-point 614 NPY = (SY + YV * DT) * AR + 100 'new screen y-point 620 PSET (OPX, OPY), 1 'move from old point 622 PSET (NPX, NPY), 0 'to new point 630 OPX = NPX: OPY = NPY 'make old point new point 640 IF XV > 0 AND NPX <= FXS THEN 610 'test for completion 650 IF XV < 0 AND NPX >= FXS THEN 610 'both directions 699 ' 700 'perform another simulation unless interrupt received from keyboard 701 ' 710 N = N + 1 'one more NEA transit completed 720 IF INKEY$ = "" THEN 800 'delay before next simulation 730 SCREEN 0, 0, 0 'unless key pressed 740 LOCATE 12, 1 'then print total transits 750 PRINT "A total of"; N; "asteroids have transited the solar disc." 760 PRINT : PRINT 'finish up 790 END 799 ' 800 'provide a random delay between transits ( 5 to 35 secs) 801 ' 810 NT = TIMER + 5 + 30 * RND 'add delay to current time 820 IF TIMER < NT THEN 820 'loop until delay time past 880 GOTO 400 'do next transit
Before running or executing the program, have a stopwatch or preferably a countdown timer on hand - set this for either 5 or preferably 10 minutes. Start the timer at the same time you start the program. Then, while watching the screen, count (either mentally tally or mark on paper) the number of simulated NEOs you observe transiting the white disc in the specified period ( 5 or 10 or more minutes).
As the last NEO (at the end of the specified period) transits the disc (ie the simulated Sun), press the keyboard spacebar (or any other key).
After a time the program will then clear the screen and display the actual number of simulated NEOs that it has generated. Compare this with the number you observed and calculate a percentage detection rate. Keep a record of this percentage and compare it with later similar values to see how you improve with practice.
This program is very simple, with a total of only 40 lines of executable code. The assumptions of rectangular uniform distribution for both velocities and direction of travel is very crude and unrealistic. When appropriate distributions for these quantities become available they could be incorporated into the code (probably with no more than a doubling of the code). Generation of bodies larger than the minimum size simulated here would require a considerable enlargement of the code, and could run into problems on older machines with maintaining an adequate real-time presentation (however, a Pentium machine should have no problem in producing a real-time display).
Novice observers may initially be inclined to doubt that their detection percentages are not closer to 100%, and may wonder if the machine is really generating all the NEOs it claims.
To produce a permanent record of each NEO transit without the "Sun", the program may be altered:
Add the line 310 GO TO 400
Delete lines 580 and 622
The NEO transits will now be written on the screen permanently as white tracks on a black background.
OBSERVATIONAL NOTES FOR A REAL-TIME NEO SOLAR TRANSIT SYSTEM
In the following discussion we will assume angular speeds of 30 to 1000 arcseconds per second, which implies a full disc diameter transit of between 2 and 60 seconds.
To detect small bodies we require maximum contrast, and uniformity of solar detail. This probably precludes H-alpha observations, as the detail apparent in H-alpha is quite large and would probably obscure a small dark body. White-light (unfiltered) images would appear to be the best. These, fortunately, are also the simplest and cheapest to produce.
A standard TV has an aspect ratio of 4:3. For optimum presentation of the solar image, the vertical direction should probably equate to about 3000 arcseconds with 2000 arcseconds for the solar disc and 500" top and bottom each for cold sky. Thus, with the standard aspect ratio, the horizontal screen direction will equate to about 4000".
Although it is now very unlikely that a scanning camera (ie employing a vidicon type camera tube) would be used for this application, it is helpful to consider such a device as a precursor to discussing a CCD camera and VCR recording devices.
In a typical TV raster, the vertical direction will be scanned by about 500 lines. Thus one line-width equates to about 6 arcseconds (we need not consider the problems of interlaced displays at this time).
In the horizontal direction, the time to scan one line is 64 microseconds (Australian PAL standard). The bandwidth of a good TV might be about 5 MHz (Black and white are better in this respect than colour). This gives a "dwell" time per "pixel" of about 0.2 us (microsecond) (1 / 5MHz) and a total of 64/0.2 of 320 "pixels" per line. Each pixel thus represents about 4000/320=12 arcseconds. A good computer monitor, by contrast, may have a video bandwidth of 20 MHz, which will give four times [about 1200 pixels] the resolution horizontally.
Now we must consider smearing due to image movement. If the image is moving too fast it will not dwell long enough in the one "pixel" for the scanning beam to register a significant change in amplitude.
Specifically, the dwell time of the object should equal the dwell time of the beam per pixel. For a pixel size of 5" this 0.1 us. If the object moves one pixel per dwell time, it will only spend 50% of the dwell time in each pixel. For maximum probability of detection (ie maximum contrast) we would ideally want the object to move at about 1/10th this speed (giving closer to 90% dwell time per pixel).
Thus, the maximum speed desired would be 5 arseconds per microsecond or 5 million arcsecond per second. This is well above the expected angular speed of any NEO and so the use of a scanning (vidicon) camera so be acceptable for solar transit NEO detection.
CCD cameras are today both very small and very cheap, and are probably the only choice for a video camera. These use a Charge Coupled Device array as the active optical detector.
The mechanism of operation is quite different to a scanning camera, as the whole array is exposed to the scene for a given time, and then read out.
For very low light levels, the exposure time may be a significant fraction of the frame/field rate (50/60 Hz). If we assume a 10% exposure time (for 50 Hz, this is 10% of 20 milliseconds, or 2 ms), then each pixel will also be exposed for 2 ms. Assuming a resolution of 5 arcseconds per pixel (as before), we want a the NEO image to move no more than one tenth of 5"/2ms or 250 arcseconds per pixel. This is still greater than the maximum NEO movement expected. Fortunately in imaging the Sun we have adequate light that exposures of less than 2 milliseconds are generally not a problem (unless we have used a filter that is too dense).
In general, the video bandwidth of the cheaper domestic VCR will not be 5 MHz, and in some odler models may only be half this value. This implies that a 5 arcsecond object may not be detected on replay. It is also likely that on fast forward (search mode), it may not be possible to a gain a very high detection probability of even much larger bodies.
The NEASOL2 simulation program presents an ideal way to examine the behaviour of VCRs in this regard. A CGA card with composite video may be recorded directly with a VCR. Higher resolution graphics adaptors use higher frequency scan rates that are not TV scompatible and thus cannot be recorded directly on a conventional VCR. There are however, video standards converters that can be purchased to convert SVGA to PAL (or NTSC), so that VCRs can be used.
Frame capture cards can also be purchased which allow video camera display (and sometimes even recording on a computer (PC). However, by careful in selection of this type of hardware and software. Most of the compression schemes that are used to bring the stored video to a reasonable file size will entirely eliminate any hope of detection of small bodies in transit of the solar disc!
NEO SOLAR TRANSIT PATROL PHILOSOPHY
At any one time the detection volume for NEOs in solar transit is a cone.
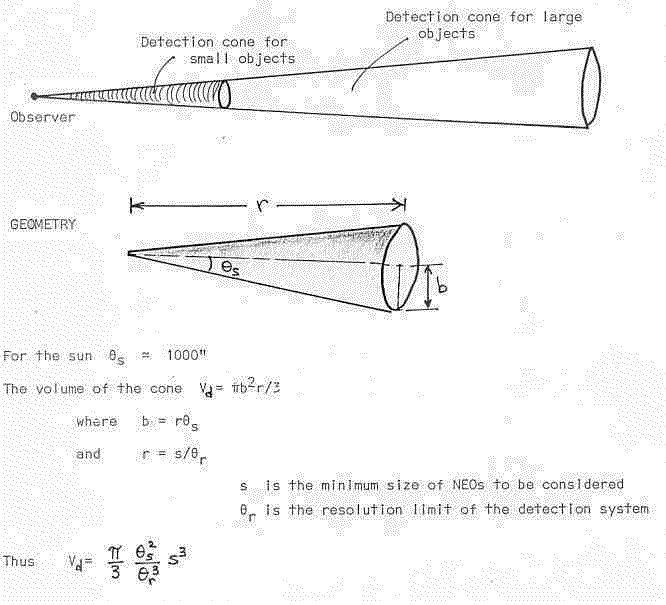
Vd is the detection cone volume for objects of size s.
To compute the number of detectable objects we might expect in this volume we need to know the volume occupied by all such objects, and the number density of these objects as a function of their size.
To try and put some numbers into our results, let us assume that the total space occupied by the majority of NEOs lies in a shell between 0.1 and 5 AU. This is a total volume of:

To find the total number of NEOs detectable within this volume we need to assume a size distribution.
Let us put this in the form:
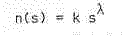
(in line with the mass distribution of the smaller meteoroids, which tends to be an inverse square mass law, we might expect the value of the size exponent lambda to be around -6)
If this number is distributed over the total NEO space, volume Vt, then we can write the number density of NEOs as:
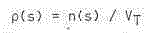
Then the total number of NEOs in our detection volume is:
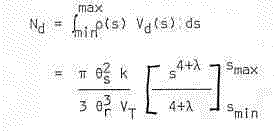
If lambda<-4 then we may let the upper limit tend to infinity and this term in the expression goes to zero, leaving us with:
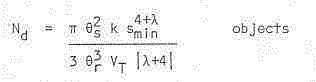
Note the critical dependence that this has on the resolution limit of our detection system. If we can reduce this from 10 arcseconds to 5 arcsecond, we octuple (increase by a factor of 8) the number of NEOs in our detection volume.
If we allow some type of average time Tbar for the Nd NEOs to clear the detection volume, then we can compute an average rate of detection of:
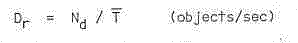
The reciprocal of Dr is the mean time between object appearances in our detection system:
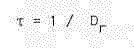
There are a lot of unknowns here that we need to guess, and of course the whole approach is very crude assuming a uniformity that is probably totally inappropraite to asteroid orbit behaviour. But let us have a look at some values that we might assign to some of the relevant quantities.
The first priority is the assumption of numbers of objects with sizes exceeding certain values (ie the size distribution law). Let us take 100m as the smallest size of concern and 10km as the largest. If we specify 100 objects exceeding 10km in size and use a size exponent of -6 we find there are 1012 objects to be found in excess of 100m in size. This would appear rather excessive and might imply that the size distribution falls off a little less steeply than an inverse square mass law would imply.
Let us however, assume a lambda=-6 size distribution law. Then for 100 objects in excess of 10km, we have a k-value of 5x1022.
The following constants are given the values:
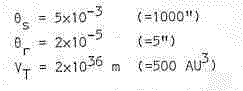
The clearing time Tbar we might estimate at around 30 seconds (the geometric mean of the minimum and maximum times to clear the detection volume).
Substituting these values inot the previous equation, we arrive at:

This would appear to be much too high to accord with reported objects transiting the Sun - observations carried out by chance. One would expect a dedicated patrol to do much better than these chance observations.
The model is obviously crude and may be out by several orders of magnitude. Unfortunately, it is more likely to be an under than a overestimate. We should also remember that very few dedicated patrol observatories (including Learmonth Solar Observatory) have ever reported small unidentified objects transiting the solar disc. The only report that I have ever been called to investigate at Learmonth turned out to be artifact within the system optics. Some solar observatories do observe regular objects passing in front of the Sun, but almost none are unidentified (an example is Big Bear, which lies near an approach path for some aircraft flying into Los Angeles).
These estimates obviously do not bode well for a succesful detection of any NEO using the solar transit method.
 Australian Space Academy
Australian Space Academy