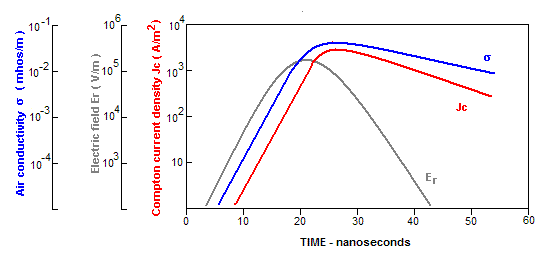
Figure 1: Curves showing conductivity, electric field and current as a function of time for a high yield (>5 megaton) weapon. For low yield weapons (kiloton), the conductivity peaks at approximately 10-4 mho/m [2]
by David Murray
The material presented here was initially written as an essay for a second year electromagnetics course given in the Newcastle University Physics Department in 1978.
INTRODUCTION
A nuclear explosion is accompanied by two principal types of electromagnetic effects. These are entirely different from each other in nature, but both involve the whole spectrum of wavelengths longer than infrared (ie from about 1 mm on up to very large values). One involves the actual emission of an electromagnetic pulse of short duration from the explosion itself or from the disturbed region in the vicinity. The other, through alteration of the electrical properties of the atmosphere, can result in serious disturbance of propagating elecromagnetic waves, such as those used in communications and for radar passing near the vicinity of the nuclear explosion. This disturbance may be caused by debris or water vapour introduced into the atmosphere by the bursts, or by the usual conditions created by the ionising radiations from the explosion. The latter mechanism may cause some radio and radar systems to be "blacked out" for several hours following the explosion.
DISTRIBUTION OF ENERGY IN A NUCLEAR EXPLOSION
The fraction of the explosion yield received as thermal energy at a distance from the burst point depends on the nature of the weapon and particularly on the environment of the explosion. For detonation in the atmosphere below an altitude of 30 km a typical value of 35% of the explosion energy is received as thermal energy; 50% of the fisson energy will be utilised in the production of blast and shock. Some 5% constitutes the initial nuclear radiations produced in the first minute after the blast. The final 10% of the total fission energy represents that of the residual (or delayed) nuclear radiation which is emitted over a period of time. This is due almost entirely to the radioactivity of the fission products present in the weapon residues (or debris) after the explosion.
It is the initial radiation, consisting mainly of gamma rays, that is of prime importance when considering electromagnetic effects.
ORIGIN OF THE ELECROMAGNETIC PULSE
There appears to be at least two different mechanisms whereby an electromagnetic pulse (EMP) may be produced by a nuclear explosion. The first is associated with the creation of radiations from the burst by some kind of asymmetry in the elecric charge distribution in the region surrounding the detonation - this is called the Compton-electron model. The second is the result of the rapid expansion of the essentially perfect conducting plasma of weapon residues in the Earth's magnetic field - this is called the field displacement model. The Compton-electron model is believed to be the principal means for generation of EMP by detonations on or slightly above the Earth's surface and by those near the 'top' of the sensible atmosphere. The field displacement model is believed to be responsible for EMP from underground bursts where the expansion is restrained in a more or less spherically symmetrical manner by the surrounding material, or from those explosions at such a great altitude that the only immediate interaction of the explosion is with the geomagnetic field.
COMPTON ELECTRON MODEL
In the Compton-electron model the photons of the initial gamma radiation leave the exploding weapon with high energies and soon collide with the electrons in the atoms and molecules of the surrounding air, and transfer to them most of their energy. These Compton electrons move rapidly away, on the average, from the centre of the burst. Provided some kind of asymmetry exists, this motion is one of the main sources of the EMP. If the exposion is perfectly symmetrical, in a uniform atmosphere, the electrical effects would be equal in all directions; the opposite components would compensate each other exactly and there would be no EMP. However, there are invariably a number of unrelated factors associated with a nuclear explosion which insures the presence of an asymmetrical system, and hence an EMP.
For surface or near surface bursts, the presence of the Earth confines expansion of the weapon residues and radiation emission to the upward hemisphere thus providing the asymmetry necessary for an EMP to be produced.
Where the explosion takes place high in the atmosphere, there will be very little interaction by upward-moving gamma rays because of low air density, whereas downward gamma rays will produce Compton electrons within a moderate distance [1].
The effect in both cases is a Compton-electron pulse which is essentially vertical. This motion of the electrons appears to be a practically instantaneously accelerated pulse of current in one direction; it is in otherwords, something like an 'electric dipole' radiator of classical electrodynamics. The current pulse in the air radiates electromagnetic energy just as it would if it were flowing in a wire transmitting antenna.
When the Compton-electrons move away from the explosion they leave behind the much slower moving positive ions, which are the other component of the electron-ion pairs. This relative displacement of positive and negative charge produces a radial electric field (figure 1).

In addition, in its passage through the air each Compton electron itself produces a large number of electron-ion pairs (~30,000), mostly at the end of its path of 3 to 4.5 m. Under the influence of the radial electric field, the large number of electrons now present will be driven back towards the burst point. This initiates a second pulse of current, but it is rapidly terminated by recombination of electrons with ions and by attachment of electrons to neutral atoms and molecules in the air, even before the electric field is neutralised. The negative ions produced in the attachment process, and a corresponding number of positive ions, remain free for a while longer (the ions being heavier and less mobile than the electrons). This large volume of ionised gas (a 'plasma') undergoes oscillations at characteristic frequencies dependent on the density of the plasma. While the oscillations last they produce electromagnetic waves in the radio frequency range [1].
The effective rise time (figure 2) of the main part of the initial signal pulse (produced by the Compton electrons) from surface or near-surface bursts is of the order of 10-8 seconds so that oscillation frequencies as high as 100 MHz ( f = 1 / T ) may be expected. However, only a very small part of the total electromagnetic energy radiated is carried at such high frequency [1].
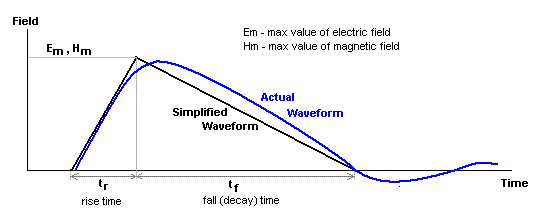
The frequency of the plasma oscillations which continue for several milliseconds and radiate considerably more energy, are much lower and are hardly attenuated at all in normal propagation, whereas the higher frequencies are much more rapidly attenuated.
The electromagnetic signal, as detected at a range of 150 km consists of a continuous spectrum with most of the energy distributed in a median frequency range from 10 to 15 kHz which is related inversely to the yield. At much longer distances (thousands of km) the form and spectrum of the pulse are determined largely by the characteristics of the medium of propagation (the Earth-ionosphere cavity) [1].
THE FIELD DISPLACEMENT MODEL
This model is considered to be of particular significance for extremely high-altitude bursts in the generation of EMP. Immediately after the detonation has occurred, the hot weapon debris is essentially a highly ionised plasma (vapour) which is rapidly expanding. A property of all plasmas is a tendency to exclude a magnetic field, such as that of the Earth, from its interior. The expanding plasma of the weapon residues thus causes a violent distortion of the Earth's magnetic field (figure 3) [1].
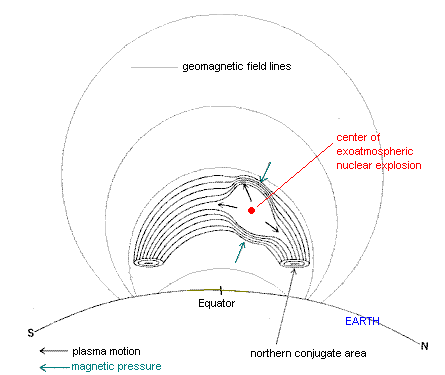
| Exoatmospheric Burst: A nuclear explosion outside the Earth's sensible atmosphere but still within its geomagnetic field, such as at several hundred kilometres altitude, results in a strong interaction between the magnetic field and the expanding ionised bomb fragments [8] |
As a result of the interaction between the geomagnetic field and the charged particles in the expanding plasma and in the very tenuous largely ionised surrounding gases, this disturbance propagates away from the burst region as a "hydromagnetic wave".
The hydromagnetic wave retains its identity and characteristics in propagating over very long distances at high altitudes, but at lower levels, where it interacts with the denser atmosphere, it is detected as an ordinary electromagnetic wave or magnetic disturbance.
This field displacement mechanism is the same mechanism that may operate to produce the EMP from an underground burst. The expansion of the debris is here limited to a few metres and the signal is therefore small, but it may be detectable at short ranges. However, it has been observed that the elecromagnetic signal from an explosion carried out at about 20 m below the ground surface was not detectable, even at very close distances [1]. This is probably because of the very large attenuation incurred in propagating through rock and soil.
PROPAGATION OF THE ELECTROMAGNETIC ENERGY
The propagation of the electromagnetic ernergy produced in a nucelar explosion, around the Earth and into space, is dependent upon the size of the source region and the height of the burst above the Earth's surface. As mentioned above, underground tests produce little, if any, detectable electromagnetic signals. At the other extreme a high yield weapon detonated at 200 km atltitude can create a source region over 1500 km in diameter and about 20 km thick, with a lower altitude limit of around 20 km. A burst of this type will cause a zone of impact of diameter 3000 km over the Earth's surface. The EMP will be reflected back and forth between the Earth and the ionosphere, propagating around the world. With each reflection energy is lost from the EMP [2].
NATURALLY PRODUCED ELECROMAGNETIC ENERGY
Before choosing a frequency to detect nuclear explosions it is necessary to determine the frequency range of naturally occuring electromagnetic emissions.
Solar flares produce electromagnetic waves that cover most of the electromagnetic spectrum. The ionosphere is transparent in only part of the radio spectrum, which permits reception of solar radio emission between about 10 MHz and 30 GHz. Below 10 MHz the ionosphere is opaque and prevents the passage of radio signals from space to the Earth. [4]
Lightning is a natural source of electromagnetic disturbance, with the following general features. At VLF (<10 kHz) a few discrete radiation pulses are emitted, associated with visual macroscopic features. As the frequency increases above the VLF band the number of pulses per discharge increases but the peak amplitude of the pulses decreases. From about 10 kHz to over 100 MHz the peak electric field intensity varies approximately inversely with frequency [3].
From the above information it is evident that lightning discharge poses a problem of distinction between itself and a nuclear EMP at VLF frequencies. Figure 4 shows a difference between the magnitude of the electric field for EMP and cloud-charge responsible for lightning. This smaller electric field will result in an elecromagnetic wave of much less energy than a nuclear detonation EMP. Hence the detectable range of lightning will be much less than that of an EMP burst.
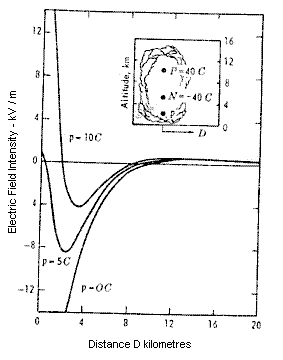
A SUITABLE FREQUENCY FOR DETECTION
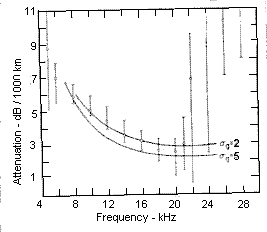
VLF signal attenuation derived from a series of nuclear test explosions is shown in figure 5. Note that attenuation rapidly increases above 20 kHz. This combined with the fact that the peak energy associated with a nuclear EMP is just around 10 kHz makes the frequency range of 10 to 15 kHz the most suitable for long range detection of nuclear explosions.
SENSORS FOR EMP MEASUREMENTS
Physical quantities, such as electric and magnetic fields, are related to the nuclear source via the source current density and the ionisation source density (electron-ion pairs per cubic metre). It is these quantities and their time derivatives that are to be measured. Three different types of sensors are commonly used.
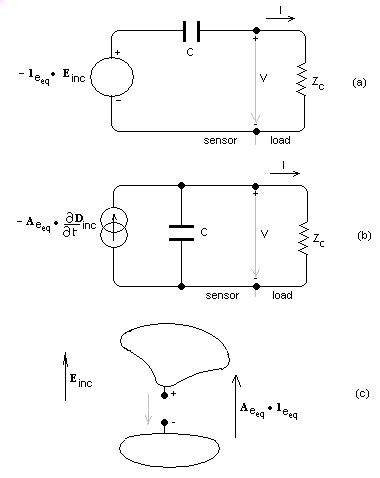
For measurement of the local electric field and its source current density an electric dipole sensor is used. The equivalent circuit is shown in figure 6. The sensor is electrically small and its load impedance is zc. The sensitivity is characterised by the sensor equivalent length le-eq which samples the incident electric field Einc. The dot product between the two vectors indicates the directional sensitivity of the sensor. An equivalent area Ae-eq samples the displacement current density. The relation between the two characterisations is given by:
To measure magnetic fields a small loop is used, which may be characterised by an inductor L (plus associated small series resistance) with an equivalent area Ah-eq (figure 7) for measurements of the magnetic field time derivative, and an associated equivalent length lh-eq which in this case are related by:
It-inc = At-eq • Jt-inc
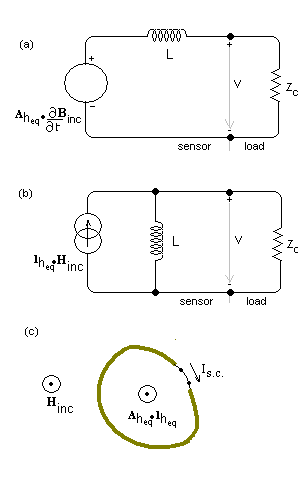 Figure 7: (after [9]). |
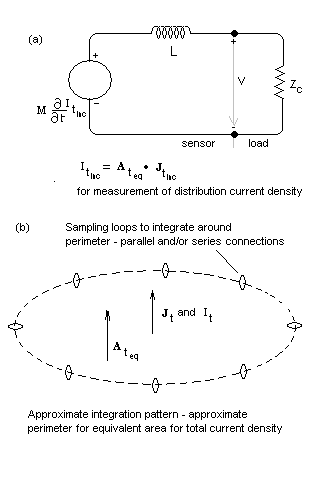 Figure 8: (after [9]). |
POWER FLOW AND APERTURE RELATIONSHIPS
For an antenna placed in the field of a linearly polarised elecromagnetic wave, the power available at the terminals under matched load conditions is given by:
| Antenna | Ae | |
|---|---|---|
|
Very short dipole Half-wave dipole Large aperture antenna Log-periodic with gain G |
1.5 λ2 / 4 π 1.64 λ2 / 4 π 50% of physical aperture G λ2 / 4 π |
COMPARISION OF DIFFERENT DETECTION SYSTEMS
Table 2 presents a brief comparison of operable detection systems setting out their uses and limitations [5].
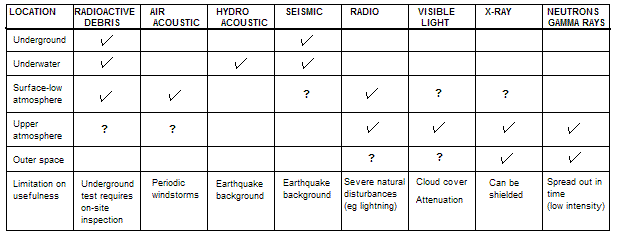
Table 3 gives the estimated detection range for a 1 Megaton detonation in space [5].
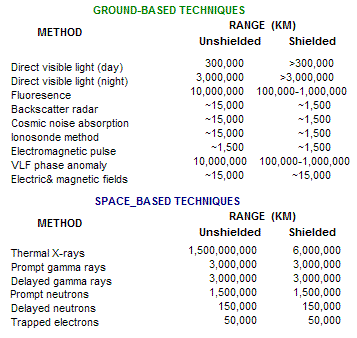
Note: A shielded explosion is one in which the nuclear device is surrounded by a sheet of lead or other material to reduce the amount of radiation emitted.
CONCLUSIONS
The electromagnetic pulse, with frequencies lying mainly in the range of 10 to 15 kHz, should enable detection of radio signals from a one kiloton explosion as far as 5,000 km away, provided there is no high background noise level in the vicinty of the receiving station. The procedure is expected to be be applicable to air bursts at altitudes up to about 1000 km. By means of radio directional equipment, the azimuthal angle of the signal could be determined with an accuracy of ~ 2 degrees; this corresponds to an uncertainty of about 30 km at a distance of 1000 km. The time of receipt of the radio signal is within a small fraction of a second of the instant of the explosion.
The great drawback of the electromagnetic detection system is that lightning flashes produce signals in about the same frequency range as the EMP from a nuclear explosion. Close to the point of detonation the characteristics of the EMP and a signal caused by lightning are quite different, but at distances over 1000 km away they are essentially the same and therefore indistinguishable with presently available equipment. Techniques are under development which may provide automatic exclusion of much of the static from lightning.

REFERENCES
 Australian Space Academy
Australian Space Academy