ROCKET NOISE (left) The first and only rocket to launch an Australian satellite (WRESAT) from Australian soil lifts off from Woomera in 1967, amid much noise, vapour and dust.

INTRODUCTION

The firing of a large rocket produces one of the most intense sounds of any man-made device. This can be physically damaging to nearby structures, let alone any biological organism.

This noise comes from the motion of the rocket's exhaust gases and their interaction with the surrounding atmosphere.

This note shows how to use simple physics to estimate the noise level of a rocket, using the experimental observation that the energy that goes into producing the audible component of the rocket exhaust is approximately one half a percent of the total mechanical energy of the exhaust.

AUDIBLE NOISE POWER

The simplest and reasonably accurate way to determine the total noise power produced by a rocket is to assume that the noise power is a fraction of the mechanical power in the exhaust:

P_noise = η P_mech

The noise from a large rocket at takeoff is one of the most intense man-made sounds you will hear.

The graph below [Ref 3] shows a plot of the above formula with varying values of η compared to real world data. A value of 0.5% efficiency (η = 0.005) seems to be the best fit.

The vertical axis of the graph is the total noise power expressed as a ratio in decibels. The reference noise power is one picowatt (10^-12). This is the smallest detectable noise an average person can hear. The sound intensity at a distance 'r' on a calm day is given by:

I_noise = P_noise / ( 4 π r² )

The units of intensity are watts per square metre. This formula is the ubiquitous inverse square law which governs the intensity of most quantities that spread out uniformly in space.

Power and intensity are generally expressed as ratios in decibels with the reference intensity being 1 picowatt per square meter:

I_noise(db) = 10 log₁₀ ( P_noise ) - 10 log₁₀ (4 π r² ) + 8

The 8 included here is because the rocket noise does not spread out omnidirectionally due to the proximity to the ground at liftoff. This focuses the noise power into less than 4π steradians (ie a full sphere), and this increases the intensity at any point above the ground.

EXHAUST MECHANICAL POWER

The mechanical power of the rocket exhaust comes from the kinetic energy produced every second.

Thus:

P_mech = dE/dt = 1/2 * dm/dt * v_e

dm/dt is the exhaust mass flow rate in kg/sec and
V_e is the exhaust velocity in metres/sec

The units of this power are Joules/sec or watts. The table below gives the exhaust velocity for different fuels:

NOISE MEASUREMENT

Noise propagates through atmosphere as a pressure wave and is perceived by the ear as a fluctuation of the ambient pressure near the ear.

Now the relationship between sound intensity and sound pressure level (SPL) is given by:

SPL = √ ( I ρ c )

ρ is the atmospheric (air) density and
c is the speed of sound

Note that this value is only accurate for sea-level and calm conditions. The presence of any wind will change this value by an amount that increases with wind speed.

The units of SPL are the units of pressure or the pascal (Pa). At ground level ρ = 1.2 kg / m³ and the speed of sound is 330 m/s. Substituting these figures in the above equation we find the reference SPL corresponding to an intensity of one picowatt per square metre is:

SPL_ref = √ ( 10^-12 * 1.2 * 330 ) = 2 x 10^-5 Pa

In decibels we find that the numerical value for the SPL (db) is the same as the numerical value for the intensity in dB. This is because they are both a ratio with their own reference levels.

This value is the number indicated by a sound level meter.

As an example we consider the Falcon 9 rocket which uses kerosene and liquid oxygen with an exhaust velocity of 2500 m/s and a mass flow rate of 1455 kg/sec.

The mechanical power generated is 4.5 x 10⁹ or 4.5 gigawatts. With a noise conversion efficiency of 0.5% the total noise power is 194 dB and the SPL at a distance of one kilometre (1000 m) is 131 dB .

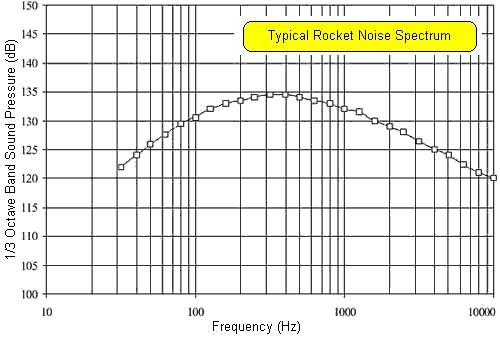
Rocket noise is broadband noise but it does have a maximum spectral power around a few hundred Hz. [Ref 3]

REFERENCES

1. NASA special publication SP-8072

2. "Rocket noise prediction models: An update",
   Louis C. Sutherland, J Acoust Soc Am, 129, 2480 (2011), https://doi.org/10.1121/1.3588162

3. "Supersonic jet noise from launch vehicles: 50 years since NASA SP-8072",
   Caroline P Lubert, Kent L Gee and Seiji Tsutsumi, J Acoustic Soc Am, 151, 752-791 (2022)